Varianta 3

Prof: Andone Elena

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului -2+12+ (-2)² este………………….

(5p)     2. Numerele de forma \(\overline{1x3}\) divizibile cu 3 sunt………………………

(5p)     3. Elementele mulţimii (-1, 4]\(\cap \mathbb{Z}\) sunt………….

(5p)     4. Fie triunghiul isoscel ABC, ABAC. Dacă măsura unghiului A este egală cu 24⁰, măsura unghiului B este egală cu……^o

(5p)     5. Dacă într-un trapez baza mică are lungimea egală cu media geometrică a numerelor 4 cm şi 9 cm şi baza mare are lungimea egală cu media aritmetică a numerelor 12cm şi 28cm, atunci lungimea liniei mijlocii va fi egală cu...cm

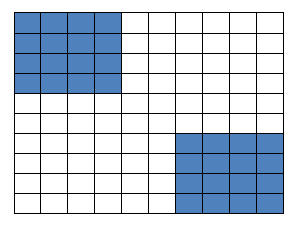
(5p)     6. Un paraşutist aterizează pe un teren asemănător desenului de mai jos. Probabilitatea ca el să aterizeze în zonă colorată este…….

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi un paralelipiped dreptunghic cu dimensiunile L5 cm, l4 cm şi h8 cm (5p)    
 (5p)    2. Determinaţi funcţia liniară al cărei grafic trece prin punctele A(1,2) şi B( -2, 1)

(5p)     3. Dacă \(\frac{x}{y}=\frac{2}{3}\)calculaţi \(\frac{7x}{7x+y}\)

           4. Moş Crăciun are în sacul său multe jucării interesante şi frumoase. Dacă ar da fiecărui copil pe care îl întâlneşte 3 jucării, ar rămâne cu 2 jucării în sac iar dacă ar da fiecărui copil câte 4 jucării, ar rămâne cu 3 jucării.

(5p)    a) Verificaţi dacă în sacul lui Moş Crăciun pot fi 107 jucării.

(5p)    b) Aflaţi câte jucării pot fi în sacul lui Moş Crăciun , ştiind că nu sunt mai mult de 350 de jucării dar nici mai putin de 300.

(5p)     5. Efectuaţi \(\frac{9{{x}^{2}}+12x+4}{16{{x}^{2}}-25}\cdot \frac{4x-5}{9x+6}\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

  1. Mădălin are un acvariu de forma unui paralelipiped dreptunghic PESCARUL, cu dimensiunile PE=50 cm, ES=40 cm, AS=50\(\sqrt{2}\)m.

 (5p)  a) Arătaţi că înălţimea acvariului este de 30 cm. 

 (5p)  b) Aflaţi distanţa de la punctul C la dreapta EU. 

 (5p)  c) Dacă în acvariu se toarnă 15 l de apă, la ce înălţime se ridică apa?

 2. Un teren  agricol  are forma unui trapez isoscel cu bazele AB şi CD , CM\(\bot \)AB   şi AC\(\bot \)BD,  AB= 18 dam , CM= 100 m. Suprafaţa acestui teren a fost împărţită în două  parcele ADCM şi BCM  .Calculaţi:                      

(5p)  a) Câţi ari are suprafaţa terenului ABCD?

(5p)  b) Cât la % din aria trapezului ABCD  reprezintă aria triunghiului BMC ?

 (5p)  c) Cât costă împrejmuirea parcelei AMCD dacă 1 m de gard costă 12,5 lei  .