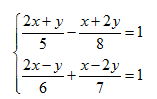Varianta 14

Prof: Badea Daniela

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1.Cel mai mic număr întreg impar de două cifre este ….

(5p)     2.Fie funcţia\(f:\left\{ -1;\text{ 0; 2; 3} \right\}\to \mathbb{R},\text{ }f\left( x \right)=x-2.\)Suma tuturor valorilor funcţiei este   egală cu …

(5p)     3.Numărul numerelor naturale cuprinse între 102 şi 201 care împărţite la 5 dau restul 3 este egal cu ….

(5p)     4.Un hexagon regulat este echivalent cu un pătrat care are perimetrul 24cm. Aria hexagonului este egală cu …. cm.

(5p)     5. Aria totală a unui tetraedru regulat este\(16\sqrt{3}\text{ c}{{\text{m}}^{\text{2}}}.\) Perimetrul bazei este de ….cm.

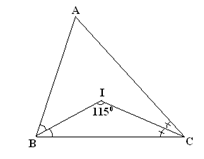
(5p)     6.În figura de mai jos (BI şi (CI sunt bisectoarele unghiurilor B şi C ale \(\Delta \text{ABC}\), iar măsura unghiului BIC este de 115⁰. Atunci măsura unghiului BAC este de ……⁰

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un tetraedru regulat MNPQ.

(5p)     2. Ionel primeşte de ziua lui o sumă de bani de la trei persoane, astfel: mama îi dăruieşte \(\frac{2}{3}\)din suma totală şi încă 5 lei, tata îi dăruieşte 60% din rest plus 3 lei, iar bunicii îi dau restul de 25 lei. Ce sumă a primit Ionel?

(5p)     3. Rezolvaţi sistemul:

           4. Fie expresia \(\text{E}\left( x \right)=\left\{ \left( x+\frac{1}{x}+2 \right):\left( 1+\frac{1}{x} \right):\left[ \left( x+\frac{1}{x}-2 \right):\left( 1-\frac{1}{x} \right) \right]-1 \right\}:\frac{8}{{{x}^{2}}-x}\)          

(5p)    a) Determinaţi valorile lui x pentru care expresia are sens şi arătaţi că \(\text{E}\left( x \right)=\frac{x}{4}\).

(5p)    b) Rezolvaţi ecuaţia \(\text{E}\left( \text{4} \right)\text{+E}\left( {{\text{4}}^{\text{2}}} \right)\text{+E}\left( {{\text{4}}^{\text{3}}} \right)\text{+}....\text{+E}\left( {{\text{4}}^{\text{2012}}} \right)\text{=}\frac{\text{4}\cdot \text{E}\left( x-1 \right)}{3}\).

(5p)     5. Determinaţi funcţia liniară al cărei grafic taie axa Ox în punctul de abscisă x=2 şi axa Oy în punctul de ordonată y= –6 .  

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Paralelipipedul dreptunghic ABCDA`B`C`D` are dimensiunile bazei AB=6cm şi respectiv BC=8cm, iar diagonala are lungimea 26cm. Calculaţi:

 (5p)   a) aria totală şi volumul paralelipipedului;

 (5p)   b) distanţa de la punctul P la dreapta BD`, unde P\(\in \)(DD`) şi \(\frac{\text{D }\!\!\grave{\ }\!\!\text{ P}}{\text{DP}}=\frac{2}{3}\);

 (5p)   c) volumul tetraedrului AMPD`, unde M este mijlocul diagonalei (BD`).

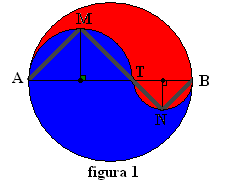
          2. Într-un parc se amenajează un rond circular cu flori. Rondul are diametrul AB=12m, iar T\(\in \)(AB) astfel încât AT=2BT. Se construiesc semicercurile \(\overset\frown{\text{AMT}}\)de diametru (AT) şi respectiv \(\overset\frown{\text{BNT}}\) de diametru (TB). Se delimitează astfel două suprafeţe pe care plantează flori roşii şi albastre (vezi figura 1). Rondul este străbătut de o alee (linie poligonală) AMTNB, lată de 50cm.

(5p)   a) Calculaţi lungimea aleii;       

(5p)   b) Calculaţi aria suprafeţei plantate cu flori roşii (se aproximează\(\sqrt{\text{2}}\simeq 1,41\)şi\(\pi \simeq \text{3,15}\));

(5p)   c) Rondul se împrejmuieşte cu arbuşti (ce vor forma un gard viu) plantaţi la 30 cm unul de altul, iar cele două straturi cu flori se delimitează în acelaşi mod. Determinaţi numărul de arbuşti necesar, dacă plantarea începe din punctul A.