Varianta 16

Prof: Badea Daniela

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \({{\left( 2-\frac{3}{2} \right)}^{2}}:\frac{1}{2}\) este egal cu ….

(5p)     2. Dacă\(2a-b=7\)şi \(4{{a}^{2}}-{{b}^{2}}=42\), atunci \(2a+b\) este egal cu ….

(5p)     3. Într-un coş sunt 35 de mere verzi şi roşii. Probabilitatea ca luând la întâmplare un măr, acesta să fie verde, este \(\frac{3}{7}\) . Numărul merelor roşii din coş este egal cu ....

(5p)     4. Lungimea laturii unui romb este medie proporţională între lungimile diagonalelor. Dacă latura are 14cm, atunci înălţimea rombului are …. cm.

(5p)     5.Pe planul dreptunghiului ABCD cu AB=20cm şi BC=15cm se ridică perpendiculara AM de 12cm. Distanţa de la punctul M la dreapta BD este de ….cm.

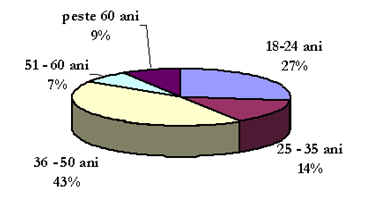
(5p)     6. La un sondaj de opinie participă un număr de persoane, în procentele indicate în diagrama alăturată, pe categorii de vârste. Diferenţa dintre numărul de persoane din categoria 36-50 ani şi numărul de persoane din categoria 18-24 ani este 352.

              La un sondaj participă ….. persoane.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1.Desenaţi, pe foaia de examen, două plane paralele\(\alpha \)şi\(\beta \), intersectate de un al treilea plan\(\gamma \), după dreptele a şi respectiv b .

(5p)     2. Calculaţi: \(\left( \sqrt{7}-\sqrt{3} \right)\left( \frac{7}{\sqrt{7}}-\frac{3}{\sqrt{3}} \right)-2\sqrt{3}\left( \frac{7}{\sqrt{12}}-\sqrt{7} \right)\).

(5p)     3. Se dă expresia\(E\left( x \right)={{\left( x-3 \right)}^{2}}+{{\left( x+1 \right)}^{2}}-2\left( x+3 \right)\left( x-1 \right)\).Rezolvaţi ecuaţia\(E\left( x \right)=0\)

           4. La o florărie s-au aranjat garoafe în 40 de vaze, în unele câte trei fire, iar în altele câte cinci fire, în total 154 fire.

(5p)    a) Aflaţi câte vaze s-au aranjat cu trei fire şi câte cu cinci fire de garoafe.

(5p)    b) Dacă se aranjează toate cele 154 de garoafe astfel ca, în fiecare vază să fie acelaşi număr de fire, aflaţi numărul minim de vaze care se utilizează ştiind că într-o vază încap cel mult 17 flori.

(5p)     5. Trasaţi graficul funcţiei \(f:\left[ -2;3 \right]\to \mathbb{R},\text{ }f\left( x \right)=1-2x.\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

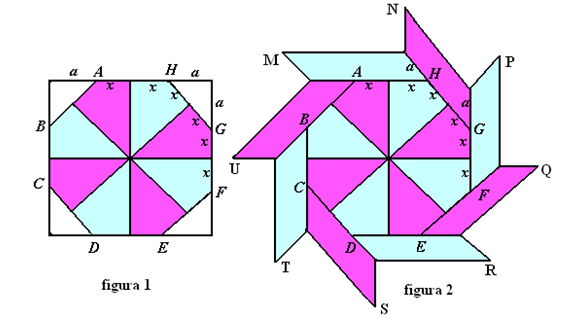
  1. Construcţia unei morişti se face în două etape: se construieşte mai întâi octogonul regulat ABCDEFGH pornind de la un pătrat (vezi figura1), apoi se lipesc cele opt paralelograme congruente,  aşa cum se vede în figura2. Se ştie că latura octogonului are lungimea 2x, iar latura pătratului 2x+2a.

 (5p)  a) Calculaţi a şi lungimea laturii pătratului în funcţie de x;

 (5p)  b) Pentru \(x=10\left( \sqrt{2}-1 \right)\text{cm}\)calculaţi perimetrul moriştii;

 (5p)  c) Pentru \(x=10\left( \sqrt{2}-1 \right)\text{cm}\)calculaţi aria moriştii.