Varianta 17

Prof: Badea Ion

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului  \(\sqrt{80}-\sqrt{245}+\sqrt{125}\) este egal cu …

(5p)     2. Un automobil parcurge o distanţă cu viteza constantă de 60km/h în 45minute. Dacă parcurge aceeaşi distanţă în 36 minute, atunci viteza automobilului va fi de ….km/h.

(5p)     3. Media geometrică a numerelor  \(3+2\sqrt{2}\) şi  \(3-2\sqrt{2}\) este egală cu …

 (5p)    4. Lungimea unui cerc este \(4\pi .\) Aria pătratului înscris în acest cerc este…

(5p)     5.Volumul unui tetraedru regulat cu muchia de 6 cm este egal cu ….cm³.

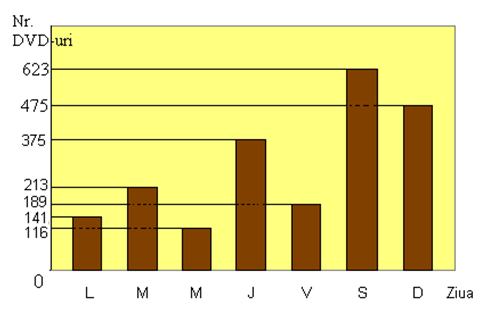
(5p)     6. În graficul alăturat se prezintă numărul de DVD-uri vândute de un magazin în cursul unei săptămâni. De marţi până vineri s-au vândut …… DVD-uri .

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, două cercuri tangente exterioare şi o tangentă comună a lor.

(5p)     2. O echipă de 10 muncitori pot executa o lucrare în 10 zile. După 3 zile de lucru s-au mai alăturat echipei încă 4 muncitori. În câte zile se va executa lucrarea?

(5p)     3. Demonstraţi că \(13|\overline{abc}\text{  }\)dacă și numai dacă\(\text{ 13}|3a-3b+c\).

            4. Se dau funcţiile \(f,g:\mathbb{R}\to \mathbb{R},f\left( x \right)=\sqrt{3}x+1\text{ i }g\left( x \right)=1-\sqrt{3}x\)

.

(5p)     a) Determinaţi coordonatele punctului de intersecţie al graficelor celor două funcţii.

(5p)     b) Aflaţi măsura unghiului format de graficele funcţiilor f şi g.

(5p)     5. Fie numărul \(A=\frac{1+\sqrt{2}-\sqrt{3}+\sqrt{7}+\sqrt{11}+\sqrt{14}-\sqrt{21}+\sqrt{77}}{1+\sqrt{2}-\sqrt{3}+\sqrt{11}}\)

. Arătaţi că \(A\in \left( 3;4 \right)\)

.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

         1. O piramidă SABCD are baza pătratul ABCD şi toate muchiile egale cu 10cm.

 (5p)  a) Demonstraţi că SABCD este piramidă regulată şi calculaţi volumul său;

 (5p)  b) Dacă punctul  \(\text{P}\in \left( \text{SC} \right)\) , determinaţi lungimea segmentului (SP) astfel încât perimetrul  \(\Delta \text{PBD}\) să fie minim;

 (5p)  c) Aflaţi măsura diedrului determinat de planele (PBD) şi (ACD).

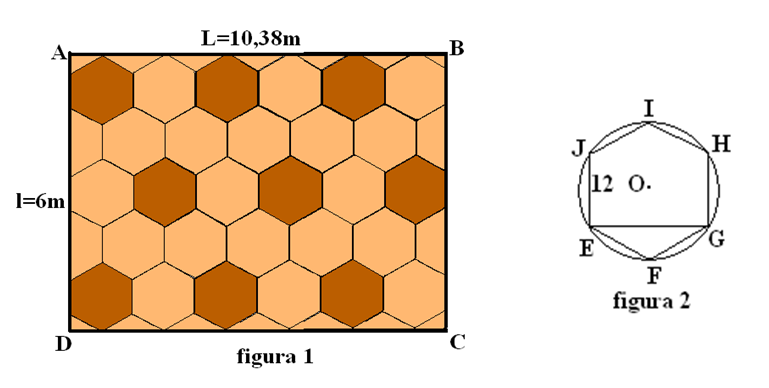
 2. O sală de conferinţe cu lungimea de 10,38m şi lăţimea de 6m trebuie pardosită cu plăci de gresie hexagonale regulate cu latura de 12cm, de două culori.

(5p)  a) Determinaţi numărul de plăci întregi de faianţă necesare dacă pardosirea începe din punctul A aşa cum arată figura 1 şi apoi numărul total de plăci necesare( se aproximează \(\sqrt{3}\cong 1,73\)).

(5p)  b) Câte plăci de culoare închisă sunt utilizate (vezi modul de aşezare în figură)?

(5p)  c) La fiecare metru pătrat se folosesc 1,2 saci cu adeziv care costă14 lei sacul. Gresia se vinde la metru pătrat care costă 30 lei, iar manopera costă 65% din preţul materialelor. Calculaţi costul total al lucrării.