Varianta 28

Prof:Breazu Nicolae

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         (30 de puncte)

(5p)     1. Rezultatul calculului \(\sqrt{12}-3\sqrt{3}-8\sqrt{3}:4+\sqrt{75}\) este...

(5p)     2. Un cioban are 50 de oi: albe şi negre. Dacă oile negre sunt de patru ori mai multe

 decât cele albe, atunci diferenţa (număr de oi negre) – (număr de oi albe) este...

(5p)     3. Dobânda la un depozit bancar pe un an este de 5%. Suma pe care o încasăm în plus,

depunând 1000 lei, după un an este de.........lei. 

(5p)     4. Aria unui hexagon regulat cu latura egală cu 2cm este de .... \(c{{m}^{2}}\).

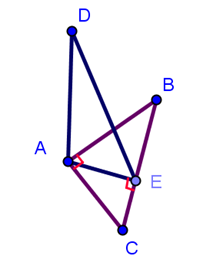
(5p)     5. În figura de mai jos dreapta AD este perpendiculară pe planul (ABC), iar \(AB\bot AC\)şi \(AE\bot BC\). Unghiul dintre dreptele DE şi BC este de ..... \(^{0}\)

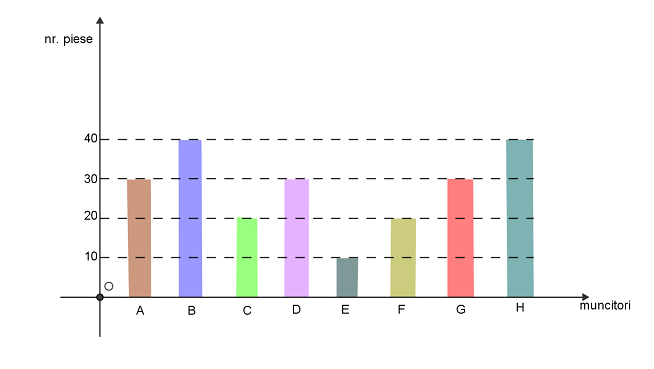
(5p)     6. În luna trecută, muncitorii unui atelier (notaţi A,B,C,D,E,F,G,H) au realizat piese

după cum arată graficul următor. Numărul total de piese realizate în acest atelier este

de....

  SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. (30 de puncte)

(5p)     1. Desenaţi pe foaia de examen un trapez dreptunghic.

(5p)     2. Să se determine mulţimea \(A=\left\{ x\in \mathbb{N}\left| \,{{\left( x+1 \right)}^{2}}-3\le 17+{{\left( x-1 \right)}^{2}} \right. \right\}.\) 

(5p)     3. Dacă la a adun de trei ori b, obţin 2,(5). Dacă din b scad de trei ori a, obţin 0,(3).

Aflaţi a şi b.

           4. Se dau funcţiile \(f,g:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=x-5,\,\,\,g\left( x \right)=-2x+1\) 

(5p)    a) Reprezentaţi grafic aceste două funcţii în acelaşi sistem de axe de coordonate; 

(5p)    b) Aflaţi coordonatele punctului comun acestor două grafice. 

(5p)     5. Arătaţi că numărul \(\frac{{{9}^{2}}}{{{3}^{5}}}:\frac{1}{\sqrt{81}}+\left( 2\frac{2}{3} \right)\cdot {{\left( \frac{\sqrt{24}}{4} \right)}^{2}}\)este natural.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.(30 de puncte)

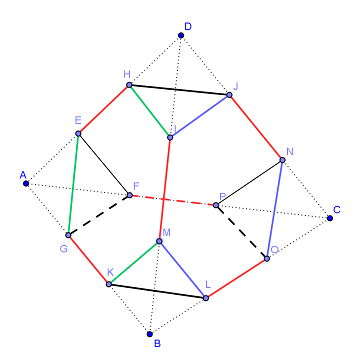
1. O piatra preţioasă în formă de tetraedru regulat cu latura de 3 cm se taie după trei feţe triunghiulare paralele cu feţele acesteia. Ştiind că cele trei tetraedre tăiate sunt de asemenea regulate, cu aceleaşi dimensiuni, se cere: 

 (5p)  a) Arătaţi că muchiile colorate în desen în roşu sunt congruente;

 (5p)  b) Ce volum total au tetraedrele înlăturate dacă feţele hexagonale obţinute sunt regulate?

 (5p)  c) Ce volum are piatra după tăiere dacă toate muchiile sunt congruente ?

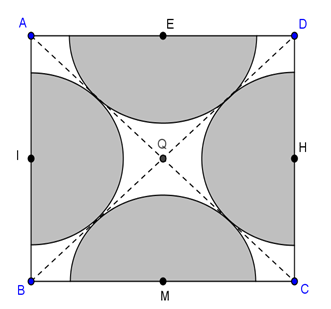
          2.  O placă de gresie are modelul ca în imagine. Ştiind că latura pătratului este de 4dm iar cele patru semicercuri cu centrele mijloacele laturilor sunt identice, tangente între ele şi tangente la diagonalele pătratului, se cere: 

(5p)  a) Să se afle raza semicercurilor; 

(5p)  b) Aflaţi aria suprafeţei nehaşurate; 

(5p)  c) Putem decupa din suprafaţa nehaşurată un cerc cu raza egală cu 1dm? Justificaţi!