Varianta 29

Prof:Breazu Nicolae

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Dacă \(x+\frac{2}{3}-4\cdot \frac{5}{16}+\frac{2}{14}:\frac{12}{7}=0\), atunci x este egal cu....

(5p)     2. Scara unui bloc are 120 de trepte. Bunicul urcă o treaptă în timp ce nepotul urcă trei

trepte. Ştiind că bunicul şi nepotul pleacă simultan şi nu se odihnesc pe drum, când ne-potul ajunge pe ultima treaptă, numărul de trepte urcate de cei doi, împreună este de....

(5p)     3. Volumul de marfă într-un depozit a fost de 14000 tone. După transferul către magazine a 30%, în depozit au mai rămas ..... tone. 

(5p)     4. Un trapez are baza mare de 8 cm iar linia mijlocie de 5cm. Baza mică are....cm.

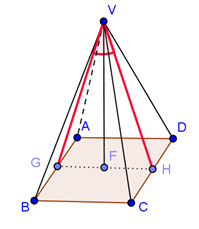
(5p)     5. În piramida patrulateră regulată VABCD notăm cu G mijlocul segmentului \(\left[ AB \right]\)şi

cu H mijlocul segmentului \(\left[ CD \right]\). Ştiind că VG=AB,  măsura unghiului \(\widehat{GVH}\) este de .....\(^{0}\).

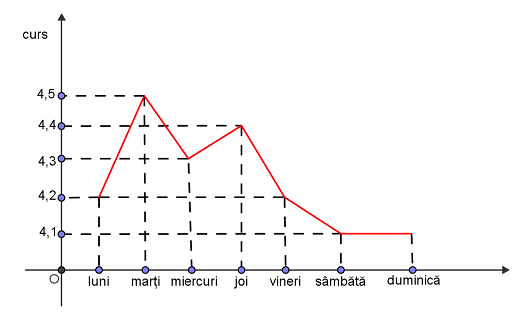
(5p)     6. Cursul de schimb euro-leu, într-o săptămână a variat după modelul din graficul ală-

turat: luni 1€= 4,2 lei, marţi 1€= 4,5 lei etc. Diferenţa dintre cea mai ridicată cotaţie şi cea mai scăzută a unui euro este de ....euro.

 SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. (30 de puncte)

(5p)     1. Desenaţi pe foaia de examen un unghi diedru şi unghiul plan al acestuia. 

(5p)     2. Calculaţi \(\left| {{x}_{1}}-{{x}_{2}} \right|\) ştiind că \(\left\{ x\in \mathbb{R}\left| 3\left( x-1 \right)={{x}^{2}}-1 \right. \right\}=\left\{ {{x}_{1}};{{x}_{2}} \right\}\). 

(5p)     3. Raportul a două numere este 0,8 iar media lor aritmetică este 4,5. Aflaţi aceste două numere. 

           4. Pentru \(x\in \mathbb{R}\backslash \left\{ \pm 1;2 \right\}\)se consideră expresia:\(E\left( x \right)=\left( \frac{x+1}{x-2}-\frac{x}{x-1} \right):\frac{2x-1}{{{x}^{2}}-x-2}\). 

(5p)    a) Arătaţi că \(E\left( x \right)=\frac{x+1}{x-1}\), oricare ar fi \(x\in \mathbb{R}\backslash \left\{ \pm 1;2 \right\}\); 

(5p)    b) Determinaţi \(a\in \mathbb{Z}\), astfel încât \(E\left( a \right)\in \mathbb{Z}\). 

(5p)     5. Dacă \(x=\frac{\sqrt{6-2\sqrt{5}}+\sqrt{6+2\sqrt{5}}}{2}\), arătaţi că \({{\left( {{x}^{2}}+x-\sqrt{5} \right)}^{2011}}-1\) este divizibil cu 4.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.(30 de puncte)

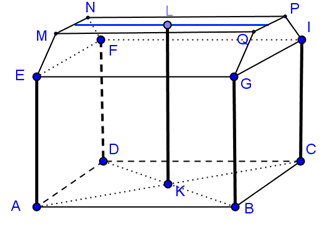
1. O hală are formă de paralelipiped dreptunghic cu L=20m, l=8m şi h=8m. Acoperişul ei are forma unei jumătăţi de prismă hexagonală care se aşează perfect pe pereţi ca în figura alăturată.   

 (5p)  a) Aflaţi volumul halei acoperite; 

 (5p)  b) În mijlocul halei este fixat un stâlp de rezistenţă. Ce înălţime are acesta? 

 (5p)  c) Pereţii exteriori şi acoperişul se vopsesc. Pentru 1\({{m}^{2}}\) este nevoie de 0,2 l vopsea. Ce cantitate de vopsea este necesară pentru toată suprafaţa?

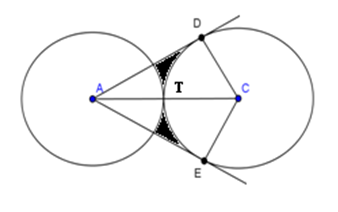
 2. Un sistem mecanic este format din două discuri de rază 10cm, tangente exterior. Din A se duc tangentele la cel de-al doilea disc. Pentru funcţionarea unui mecanism în care este implicat acest sistem sunt foarte importante suprafeţele cuprinse între tangente şi cercuri. 

(5p)  a) Determinaţi lungimea tangentelor AD şi AE; 

(5p)  b) Care este suma ariilor suprafeţelor haşurate; 

(5p)  c) Calculaţi raza discurilor în cazul în care suma ariilor suprafeţelor haşurate este egală cu 0,5 \(c{{m}^{2}}\).