Varianta 30

Prof:Breazu Nicolae

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         (30 de puncte)

(5p)     1. Media aritmetică a numerelor 19, 25 şi 46 este....

(5p)     2. Două bile sunt aruncate simultan din vârful unui turn. Prima bilă este de 4 ori mai grea decât a doua şi atinge solul după 4 secunde de la aruncare. A doua bilă atinge so-lul după.... secunde de la aruncare.

(5p)     3. Dacă a=300, atunci 5% din 20% din a înseamnă.... 

(5p)     4. Un romb are lungimea laturii de 3 cm iar un unghi de \({{30}^{0}}\). Aria rombului este de....  \(c{{m}^{2}}\).

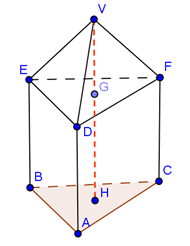
(5p)     5.  Deasupra unei prisme triunghiulare regulate ABCDEF având muchia bazei egală cu înălţimea de 3 cm se aşează un tetraedru regulat VDEF . Înălţimea VH a corpului obţinut este de....cm.

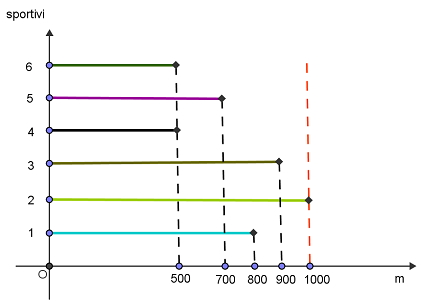
(5p)     6. În momentul atingerii liniei de sosire de primul sportiv, la proba de caiac-canoe, clasamentul era cel marcat în graficul de mai jos. Având în vedere că ordinea atingerii liniei de sosire nu s-a schimbat, locurile 1,2 şi 3 au fost ocupate de sportivii de pe cu-loarele:  .... , ..... , ......

  SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. (30 de puncte)

(5p)     1. Desenaţi pe foaia de examen un triunghi isoscel având un unghi obtuz. 

(5p)     2. Găsiţi valoarea minimă a expresiei \(E=\sqrt{4{{x}^{2}}-12x+10}+\left| 3-5y \right|\), dacă \(x,y\in \mathbb{R}\). 

(5p)     3. Numerele reale a,b sunt direct proporţionale cu 3 şi 7. Ştiind că \(2a+4=b\), aflaţi a şi b. 

           4. Se dă funcţia \(f:\mathbb{R}\to \mathbb{R}\,\,\,f\left( x \right)=\left( a-1 \right)x+a\). 

(5p)    a) Aflaţi a pentru care A(a;16) aparţine graficului funcţiei f; 

(5p)    b) Pentru a=2, calculaţi \(f\left( 1 \right)+f\left( 2 \right)+...+f\left( 20 \right)\). 

(5p)    5. Arătaţi că numărul \(\left( 2-\frac{1}{2} \right)\cdot {{\left( 2-\frac{1}{2} \right)}^{2}}:{{\left( 2-\frac{1}{2} \right)}^{3}}\cdot {{\left( 2-\frac{1}{2} \right)}^{4}}:{{\left( 2-\frac{1}{2} \right)}^{5}}\cdot ...:{{\left( 2-\frac{1}{2} \right)}^{2011}}\) este subunitar.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete. (30 de puncte)

       1. O seră are forma unui cub cu latura de 3m. În centrul de greutate al acestui corp se fixează o sursă de lumină legată prin cabluri de cele patru colţuri ale tavanului.  

 (5p)  a) Care este cosinusul unghiului pe care îl face orice cablu cu planul tavanului? 

 (5p)  b) Care este lungimea totală a cablurilor folosite? 

 (5p)  c) Arătaţi că dacă în seră sunt lăsaţi să zboare 28 de fluturi, atunci există doi fluturi la o

distanţă mai mică de 1,8m unul de altul.

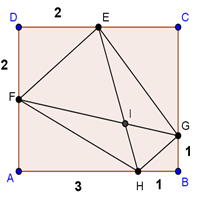
      2. O piesă metalică trapezoidală se decupează dintr-un material dreptunghiular.

Având în vedere dimensiunile precizate în desen. 

(5p)  a) Calculaţi lungimile bazei mari, bazei mici şi a laturilor neparalele; 

(5p)  b) Se perforează piesa în punctul de intersecţie a diagona-lelor trapezului. La ce distanţă de vârfurile piesei este această gaură? 

(5p)  c) Determinaţi aria piesei trapezoidale.