Varianta 32
Prof: Bulgăr Delia Valentina
- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.
- Timpul efectiv de lucru: 2 ore.
SUBIECTUL I – Pe foaia de examen se trec doar rezultatele. ( 30 de puncte)
(5p) 1. Rezultatul calculului 13-13·2+10·7 este numărul………….
(5p) 2. Media aritmetică a numerelor 3,7 şi 7,3 este……………
(5p) 3. După o scumpire cu 25% o bicicletă costă 480 lei. Preţul iniţial al bicicletei a fost
de………… lei.
(5p) 4. Dacă aria unui triunghi echilateral este egală cu 25\(\sqrt{3}\)\(c{{m}^{2}}\), atunci perimetrul
triunghiului este egal cu……… cm.
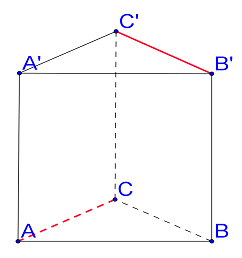
(5p) 5. Se consideră prisma triunghiulară regulată dreaptă ABCA´B´C´ din figura 1.
Măsura unghiului dintre dreptele AC şi B´C´ este egală cu……… \(^{o}\).
figura 1.
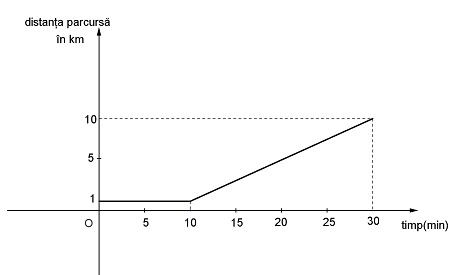
(5p) 6. În graficul din figura 2. este reprezentată lungimea drumului parcurs de un elev în funcţie de timp. Elevul aşteaptă autobusul timp de …….. min.
figura 2.
SUBIECTUL II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)
(5p) 1. Desenaţi, pe foaia de examen, o piramidă triunghiulară regulată de vârf V şi bază ABC.
(5p) 2. Se dă \(\frac{a}{b}=0,(6)\). Să se calculeze \(\frac{2a+3b}{3b}\).
(5p) 3. Mergând la şcoală cu maşina şi întorcându-se apoi pe jos, un elev face aceste drumuri în 45 de minute. Dacă face ambele drumuri cu maşina îi sunt necesare 20 minute. Aflaţi în cât timp face elevul drumul până la şcoală dus-întors.
4. Fie f:\(\mathbb{R}\to \mathbb{R}\),f(x)=2x-2.
(5p) a) Reprezentaţi grafic funcţia f.
(5p) b) Aflaţi coordonatele punctelor de intersecţie ale graficului funcţiei cu axele de
coordonate.
(5p) 5. Fie x=\(\frac{2}{a}\cdot \left( \sqrt{1-2a+{{a}^{2}}}+\sqrt{1+2a+{{a}^{2}}} \right)\)şi a>1. Arătaţi că \(\sqrt{x}\in \mathbb{Z}\).
SUBIECTUL III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)
1. Într-un acvariu sub forma unui paralelipiped dreptunghic cu L= 50cm, l= 40cm şi h=3dm se toarnă 35litri apă.
(5p) a) La ce înălţime se ridică apa turnată în acvariu?
(5p) b) Câtă apă mai trebuie adăugată pentru ca acvariul să se umple complet?
(5p) c) Câte cubuleţe cu latura de 2 cm încap în acvariul gol?
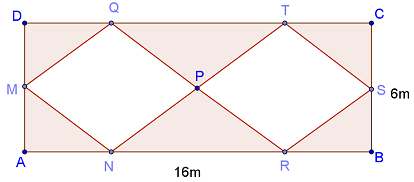
2. Figura 3. reprezintă schiţa a două rondouri de flori, sub formă de romburi identice,
aflate în interiorul unei grădini dreptunghiulare şi care au vârful P în comun, iar
celelalte vârfuri sunt situate pe laturile dreptunghiului. Se ştie că AB=16m şi
BC=6m.
(5p) a) Calculaţi suprafaţa unui rondou.
(5p) b) Arătaţi că aria porţiunii haşurate este egală cu suprafaţa rondourilor.
(5p) c) Arătaţi că oriunde am planta doi copaci în zona haşurată, distanţa dintre aceştia este
mai mică decât 18m.
figura 3.