Varianta 34

Prof:Bulgăr Delia Valentina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului -5+6:2 este egal cu……………….

(5p)     2. Dacă un plic de 150g de fertilizant este recomandat pentru o suprafaţă de 800m\(^{2}\),

                atunci pentru a fertiliza o suprafaţă de 1600m\(^{2}\) sunt necesare …….. plicuri de 150g.

(5p)     3. La concursul de matematică au participat 6 elevi din clasa noastră, ceea ce

                reprezintă 22,(2)% din efectivul clasei. În clasa noastră sunt………elevi.

(5p)     4. Un triunghi echilateral are semiperimetrul de 18cm. Latura triunghiului echilateral

                este de ……….cm.

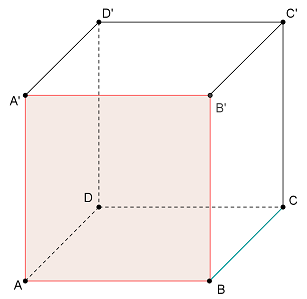
(5p)     5. Se consideră cubul ABCDA’B’C’D’ din figura1.Măsura unghiului dintre dreapta 

               BC şi planul (AA’B) este de ………….\(^{\circ }\).

figura 1.

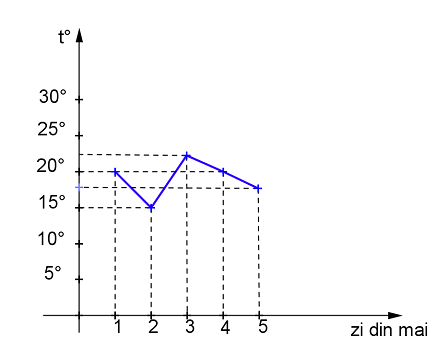
(5p)     6. În graficul din figura 2. sunt reprezentate temperaturile din primele 5 zile ale lunii

                mai. Cea mai friguroasă dintre zile a fost ziua de………..mai.

figura 2.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o piramidă patrulateră regulată dreaptă de vârf  S şi  

                bază MNPQ.

(5p)     2. Un fermier creşte găini şi iepuri. Ştiind că dacă le numără capetele obţine 20, iar

               dacă le numără picioarele obţine 64, aflaţi câte găini şi câţi iepuri are fermierul.

(5p)     3. Calculaţi valoarea numărului a=\(-\sqrt{3}-3\sqrt{12}+4\sqrt{27}-5\sqrt{48}+3\sqrt{75}\)

            4. Fie funcţia f:[-5,4]\(\to \mathbb{R}\), f(x)= 4-2x.

(5p)    a) Reprezentaţi grafic funcţia.

(5p)    b) Rezolvaţi ecuaţia f(x)-2\(\sqrt{2}\)= 4

(5p)     5. Arătaţi că E(n)=\(({{n}^{2}}+2n-3)({{n}^{2}}+2n-5)+1\) este pătrat perfect, oricare ar fi n\(\in \mathbb{N}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Andrei locuieşte într-un bloc care are forma unei prisme patrulatere regulate drepte, cu  latura bazei de 16m şi înălţimea egală cu \(\frac{3}{2}\)din lungimea laturii bazei. Blocul are un acoperiş în formă de piramidă patrulateră regulată dreaptă cu înălţimea egală cu \(\frac{1}{4}\)din lungimea laturii bazei.

 (5p)  a) Calculaţi suprafaţa laterală a blocului.

 (5p)  b) Calculaţi lungimea muchiei laterale a acoperişului.

 (5p)  c) Calculaţi numărul de ţigle necesare pentru acoperiş, ştiind că pentru 1m\(^{2}\)se folosesc 

              20 de ţigle(rotunjiţi rezultatul la întreg).

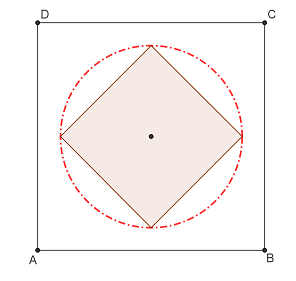
        2.  În figura 3. este reprezentată placa unei mese sub formă de pătrat cu latura de 135cm,

            acoperită de o faţă de masă rotundă, circulară, cu raza de 45\(\sqrt{2}cm\), astfel încât centrul 

            cercului coincide cu centrul pătratului.

(5p)  a) Calculaţi suprafaţa acoperită de faţa de masă (\(\pi \)=3,15).

(5p)  b) Ce suprafaţă de masă rămâne neacoperită ?

(5p)  c) Deoarece furnirul de pe placă s-a pătat, proprietarul hotărăşte să înlocuiască partea 

            din lemn haşurată cu plăci pătratice din marmură cu latura de 30cm. Dacă  o placă îl 

            costă 32 lei, montarea fiind inclusă în preţ,  cât îl costă întreaga înlocuire?

figura 3.