Varianta 38

Prof: Burlăciuc Maria

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\sqrt{128}:\sqrt{2}\) este egal cu ..............

(5p)     2. Dacă produsul a două numere naturale este 540, iar c.m.m.m.c. al lor este 180, atunci c.m.m.d.c. al celor două numere este egal cu …………

(5p)     3. Cel mai mic număr întreg din intervalul  \(\left( -5;12 \right]\)este egal cu …… 

(5p)     4. Dacă \(\vartriangle ABC\sim \vartriangle MNP\), AC =6 cm şi MP= 12 cm, atunci raportul dintre aria triunghiului ABC şi aria triunghiului MNP este egal cu ….......

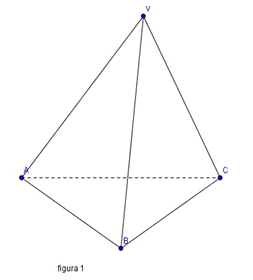
(5p)     5. În figura 1 este reprezentată piramida triunghiulară VABC. Dacă aria triunghiului VBC este de 25 cm², atunci aria laterală a piramidei este egală cu …… cm²

(5p)     6. Media aritmetică ponderată a numerelor 5; 6 şi 7 având ponderile 2; 3 şi respectiv 5 este egală cu  ………

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o prismă dreaptă THALES cu baza THA triunghi echilateral. 

(5p)     2. Dacă \(\frac{a}{b}=\frac{2011}{2012}\), calculaţi valoarea raportului \(\frac{2a-b}{b-a}\). 

(5p)     3. Determinaţi numărul natural n pentru care fracţia \(F=\frac{{{3}^{n+2}}+4\cdot {{3}^{n+1}}+2\cdot {{3}^{n}}+149}{2012}\) este echiunitară.

           4. Se consideră funcţia  f:R\(\to \)R, \(f\left( x \right)=3x+2\). 

(5p)    a) Reprezentaţi grafic funcţia f în sistemul de coordonate xOy. 

(5p)    b) Arătaţi că \(f\left( n \right)\cdot f\left( n+2 \right)+9\) este pătrat perfect, \(\forall \)\(n\in \)N. 

(5p)     5. Dacă \(x+\frac{1}{x}=5\), calculaţi \({{x}^{3}}+\tfrac{1}{{{x}^{3}}}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

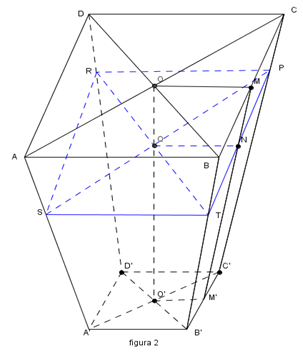
  1. O vază de flori în formă de trunchi de piramidă patrulateră regulată ABCDA’B’C’D’ are AB = 20cm, A’B’= 10 cm şi înălţimea de  30 cm (figura 2) .

 (5p) a) Determinaţi volumul vazei

(5p)  b) Determinaţi câţi litri de apă trebuie puşi în vază pentru ca apa să se ridice la o înălţime de 24 cm.

 (5p)  c) Determinaţi distanţa de la O la planul (BC C’).

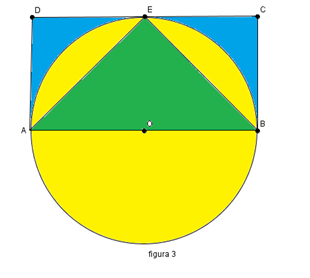
          2. Maria deseneaza pe un carton  un dreptunghi ABCD cu AB = 10 cm şi BC = 5 cm, apoi trasează cercul circumscris triunghiului ABE, unde E este mijlocul laturii CD. Colorează triunghiul ABE cu verde, porţiunea ramasă din cerc o colorează cu galben, iar porţiunea  ramasă necolorată din dreptunghi  o colorează cu albastru. 

(5p)  a) Demonstraţi că  triunghiul AEB este dreptunghic şi determinaţi aria acestuia.

 (5p)  b) Determinaţi suprafaţa colorată cu galben. 

(5p)  c)  Arătaţi că suprafaţa colorată cu albastru este mai mică decât 11 cm².