Varianta 52

Prof: Ciocǎnaru Viorica

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului: 12\(\sqrt{2}\) - 2 -  4\(\sqrt{18}\)este ........

(5p)     2. La o lucrare s-au acordat 5 note de 10, 4 note de 9, 10 note de 7, 6 note de 4 şi 2 note de 3. Procentul notelor sub 5 este ....

(5p)     3. Un romb are unghiurile ascuţite cu mǎsura de 60⁰. Un unghi obtuz al rombului are mǎsura de .....

(5p)     4. Un tetraedru regulat are muchia de 8 cm. Aria sa lateralǎ este ..... cm².

(5p)     5. Diagonala unui dreptunghi cu lǎţimea de 9 cm are 15 cm. Aria dreptunghiului este   .... cm².

(5p)     6. O piramidǎ patrulaterǎ regulatǎ are muchia bazei de 12 cm şi înǎlţimea egalǎ cu muchia bazei bazei. Apotema piramidei este .... cm.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o prismǎ triunghiularǎ dreaptǎ GALBEN cu baza inferioarǎ GAL.

(5p)     2. Fie A = {x \(\in \)R|  |x - 3| < \(\sqrt{2}\)} şi B = {x \(\in \)R|  |2x + 1| \(\le \) 5}. Determinaţi A \(\bigcap{{}}\)B.

(5p)     3. Şase covrigi şi şapte pâini costǎ 11,4 lei iar pentru şapte covrigi şi şase pâini s-au Plǎtit 10,7 lei. Preţul unui covrig este .... lei iar preţul unei pâini este .... lei.

 4. Se considerǎ punctele de coordonate A (2, -6) şi B (-5, -9).

(5p)    a). Determinaţi funcţia f : R \(\to \) R, f(x) = ax + b ştiind cǎ punctele A şi B aparţin graficului funcţiei.

(5p)    b). Aflaţi coordonatele punctelor în care graficul funcţiei taie axele Ox şi Oy.

(5p)     5. Calculaţi \(\sqrt{xy}\) unde x = (\(\sqrt{3}-\sqrt{2}\))² şi y = \(\sqrt{2}\)(\(\sqrt{2}\) + 2\(\sqrt{3}\)) +3.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Într-un rezervor, sub formǎ de trunchi de piramidǎ patrulaterǎ regulatǎ cu muchiile bazelor de 10 m şi respectiv 8 m, se aflǎ apǎ care se ridicǎ la 6 m înǎlţime.

 (5p)  a). Determinaţi lungimea muchiei laterale a trunchiului de piramidǎ.

 (5p)  b). Aflaţi înǎlţimea piramidei din care provine trunchiul.

 (5p)  c). Se goleşte rezervorul într-un bazin sub formǎ de piramidǎ patrulaterǎ regulatǎ cu vârful în jos. Aflaţi înǎlţimea la care se ridicǎ apa în bazin, dacǎ suprafaţa apei este un pǎtrat cu aria de 183 m².

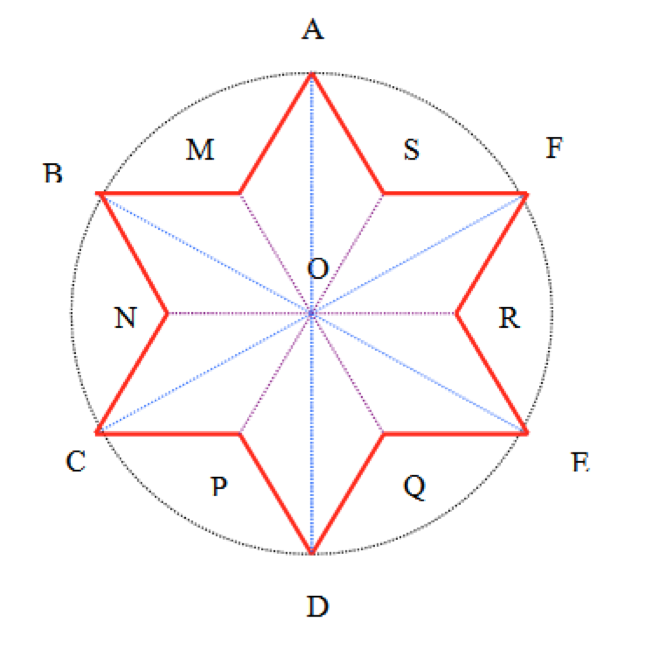
2. Un elment ornamental prezent în pictura ceramicii populare este redat în  figura de mai jos. Cercul are raza R = 6\(\sqrt{3}\) cm. Unghiurile la centru de tipul \(\angle \) AOM sunt congruente. Punctele M, N, P, Q, R, S sunt conciclice, OM = 6 cm.

(5p)  a) Care este mǎsura unghiurilor la centru de tipul \(\angle \) AOB? Dar mǎsura unghiurilor la centru de tipul \(\angle \) MOR?

(5p)  b). Care este aria figurii AMBNCPDQERFS?

(5p)  c). Care este perimetrul figurii AMBNCPDQERFS şi raportul între acesta şi lungimea cercului de razǎ OA?