Varianta 53

Prof: Ciocǎnaru Viorica

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului: 12\(\sqrt{2}\) – 2\(\sqrt{3}\) + \(\sqrt{12}\) - 3\(\sqrt{32}\) este ........

(5p)     2. La o lucrare s-au acordat la o clasǎ 8 note de 10, 4 note de 9, 10 note de 7 şi 2 note de 6. Media clasei este ....

(5p)     3. Un triunghi dreptunghic are ipotenuza cu lungimea de 11 cm şi un unghi ascuţit cu mǎsura de 30⁰. Cateta care se opune unghiului de 30⁰ este de .... cm.

(5p)     4. Dupǎ ce a cheltuit 25% din suma pe care o avea, un tânar a rǎmas cu 18 lei. Suma pe care a avut-o la început este ....

(5p)     5. Un paralelogram are laturile cu lungimile de 12 şi de 8 cm şi unghiul dintr ele de

300. 30⁰. Aria sa este .... cm².

(5p)     6. Un cub are aria totalǎ 96 cm². Volumul sǎu este .... cm³.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen conul circular drept cu secţiunea axialǎ ARC şi vârful conului A.

(5p)     2. Pentru a confecţiona 3 bluze şi 5 rochii, o croitoreasǎ foloseşte 17 m de material, iar pentru a confecţiona 4 bluze şi 3 rochii, ea utilizeazǎ 13,5 m de material. Câţi metri de material intrǎ într-o bluzǎ şi câţi metri de material intrǎ într-o rochie?

(5p)     3. Rezolvaţi ecuaţia \(\frac{2x+0,2(6)}{2}=1,(3)\), unde x \(\in \) R.

 4. Se considerǎ expresia E(x) = \(\frac{{{(x-1)}^{2}}+{{(x-1)}^{2}}-6}{{{x}^{2}}+1}\), unde x\(\in \)R.

(5p)    a). Aduceţi expresia la forma cea mai simplǎ şi rezolvaţi ecuaţia E(x) = 0.

(5p)    b). Calculaţi E(1), E(\(\sqrt{3}\))/\(\sqrt{3}\)  .

(5p)     5. Se ştie cǎ \(\frac{a}{b}\) = 3 -\(\sqrt{5}\). Calculaţi raportul \(\frac{{{a}^{2}}+{{b}^{2}}}{ab}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

       1. Globurile de Crǎciun se transportǎ în cutii sub formǎ de prismǎ dreaptǎ cu baza pǎtrat, sau în cutii cilindrice. Cutiile prismatice au latura pǎtratului de 10 cm şi înǎlţimea de 15 cm, cutiile cilindrice au diametrul bazei de 5 cm şi înǎlţimea de 60 cm, iar globurile sunt sferice cu diametrul de 4,8 cm.

 (5p)  a). Determinaţi ariile totale ale cutiilor prismaticǎ şi cilindricǎ.

 (5p)  b). Calculaţi volumele celor douǎ tipuri de cutii.

 (5p)  c). Câte globuri intrǎ într-o cutie? Calculaţi volumul unui glob şi raportaţi volumul cutiei prismatice la volumul cutiei cilindrice.

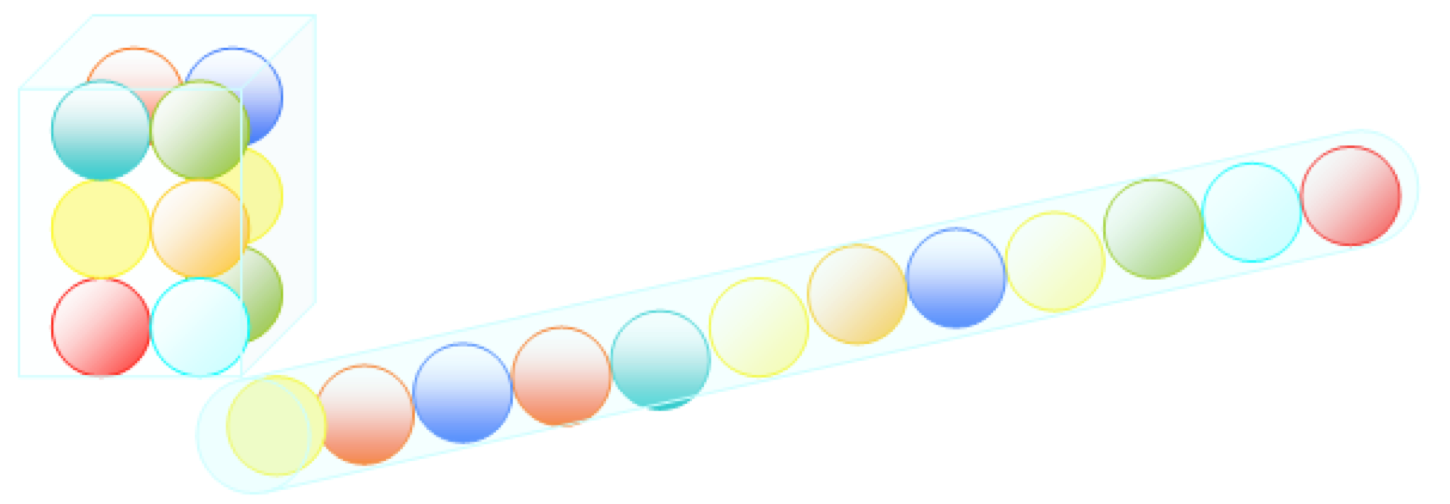
 2. Un element decorativ geometric este format dintr-un pǎtrat cu latura de 6 dm.  Fiecare laturǎ se împarte în câte trei segmente congruente. Pe segmentele din mijloc se construiesc triunghiuri isoscele cu vârfurile în centrul de simetrie al pǎtratului iar în exteriorul pǎtratului triunghiuri echilaterale congruente.

(5p)  a) Calculaţi aria triunghiurilor formate.

(5p)  b) Determinaţi raportul perimetrul pǎtratului şi perimetrul triunghiurilor isoscele.

(5p)  c) Ce procent reprezintǎ aria triunghiurilor isoscele din aria pǎtratului?