Varianta 55

Prof: Cocalea Rodica

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(26-25:(-5)\) este egal cu ....

(5p)     2. Numerele întregi din intervalul  [-4, 5) sunt în număr de ....

(5p)     3. După o reducere de 20% o bluză costă 24 lei. Preţul iniţial al bluzei a fost de ... lei.

(5p)     4. Aria unui pătrat cu diagonala de \(2\sqrt{2}\)cm este egală cu …….cm².

(5p)     5. Volumul unei prisme patrulatere regulate cu muchia bazei de 5 cm şi înălţimea de x cm este egal cu 75 cm³. Valoarea lui x va fi egală cu ... cm.

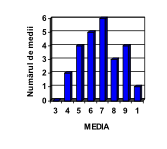
 (5p)     6. Pe semestrului al II-lea, elevii clasei a VIII-a A au obţinut mediile la matematică  conform diagramei alăturate. Numărul total de elevi cu  medii mai mari sau egale cu 7 este egal cu ....

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un tetraedrul care are baza ABC şi vârful D.

(5p)     2. Dacă numerele întregi \(x,y\)şi \(z\)verifică egalitatea \(2x-3y-10z=0\), atunci arătaţi     că produsul \(y(x+z)\) se divide cu 6.

(5p)     3. Trei numere raţionale sunt invers proporţionale cu numerele 0,5, 0,(3) şi 0,25. Ştiind    că media aritmetică a lor este 27, să se determine numărul cel mare.

 4. Fie funcţia \(f:R\to R,f(x)=-2x+4\).

(5p)    a) Calculaţi \(f(0)-3\cdot f(-1)\).

(5p)    b) Reprezentaţi grafic funcţia \(f\).

(5p)     5. Dacă \(a\in {{R}^{*}}\)şi \(a-\frac{1}{a}=12\), atunci calculaţi\({{a}^{2}}+\frac{1}{{{a}^{2}}}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O cutie de carton ABCDA'B'C'D' în formă de cub are muchia de 6 dm.

 (5p)  a) Câţi metri pătraţi de carton sunt necesari pentru confecţionarea a 120 de cutii?

 (5p)  b) Stabiliţi câte cutiuţe în formă de cub cu latura de 15 cm intră într-o cutie de carton.

 (5p)  c) În cutia de carton se aranjează cutiuţe în formă de paralelipipede dreptunghice care   au dimensiunile numere naturale consecutive, exprimate în centimetri. Care este numărul maxim de cutiuţe care se poate  aranja, dacă dorim ca volumul cutiuţei să fie  cât mai mare?

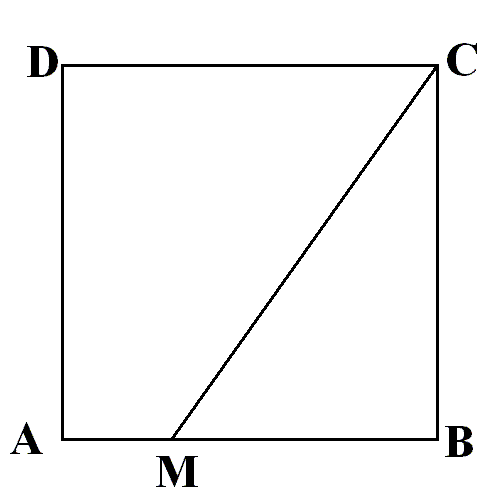
 2. În figura alăturată aveţi pătratul ABCD cu latura de 12 cm. Punctul M aparţine segmentului [AB] astfel încât BM = x.

(5p)  a) Aflaţi aria patrulaterului  AMCD în funcţie de x.

(5p)  b) Aflaţi valoarea lui x astfel încât aria triunghiului MBC să fie o pătrime din aria pătratului ABCD.

(5p)  c) O furnicuţă porneşte din punctul D şi ajunge pe dreapta MC. Ce lungime are drumul cel mai scurt al furnicuţei?