Varianta 60

Prof: Constantin Corina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(218:2-9\) este egal cu ...

(5p)     2. Numerele de forma \(\overline{23x}\vdots 2\), pentru care \(x>4\), sunt ...

(5p)     3. Cel mai mare divizor comun al numerelor 84 şi 98 este ...

(5p)     4. În paralelogramul ABCD, diagonala AC = 8 cm şi distanţa de la punctul D la AC este de 4 cm. Aria paralelogramului este de ... cm².

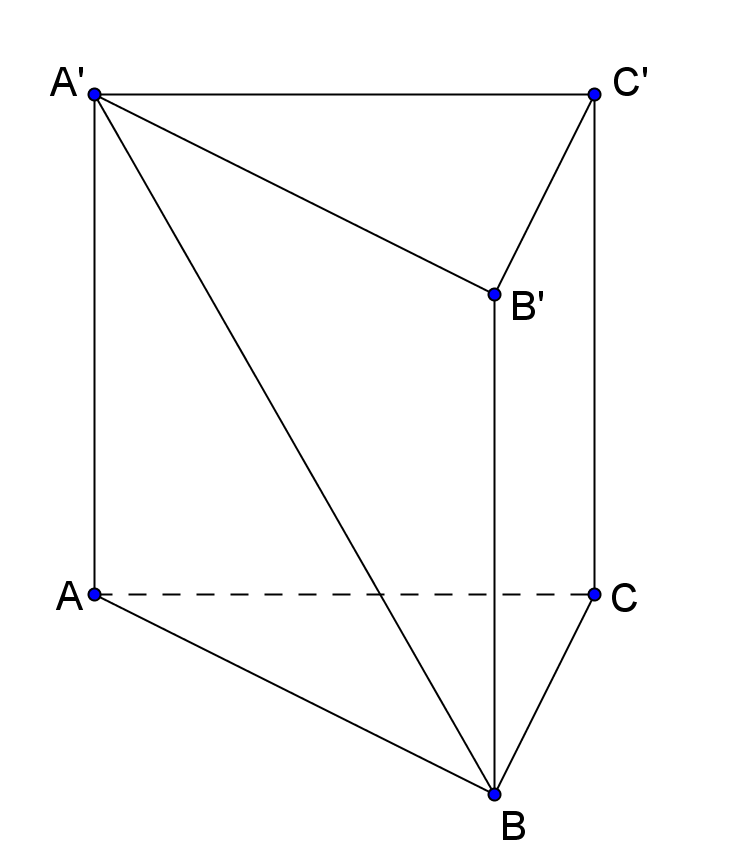
Figura 1

(5p)     6. În tabelul de mai jos, sunt date temperaturile, în grade C, pe zile, într-o săptămână friguroasă de iarna.

Temperatura medie este de ... ⁰C.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un tetraedru VABC.

(5p)     2. Într-o ladă sunt 415 mere. Ştiind că se pun câte 15 mere în 27 de pungi, aflaţi câte mere au rămas în ladă.

(5p)     3. Din Carrefour, o persoană cumpără 5 kg de mere golden şi 4 kg de portocale, pentru care plăteşte 20,50 lei. O altă persoană cumpără din acelaşi loc 6 kg de mere golden şi 8 kg de portocale, pentru care plăteşte 31 lei. Cât costă 1 kg de mere golden şi cât unul de portocale?

 4. Fie funcţiile \(f:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=x+2\) şi \(g:\mathbb{R}\to \mathbb{R}\), \(g\left( x \right)=2x+1\).

(5p)    a) Determinaţi coordonatele punctului de intersecţie al graficului funcţiei f cu axa absciselor.

(5p)    b) Determinaţi coordonatele punctului de intersecţie al graficelor celor două funcţii.

(5p)     5. Arătaţi că \(\frac{2x+34}{x-3}:\left( \frac{5}{x-3}-\frac{4}{x+1} \right)=2x+2\), pentru \(x\in \mathbb{R}-\left\{ -1,3 \right\}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

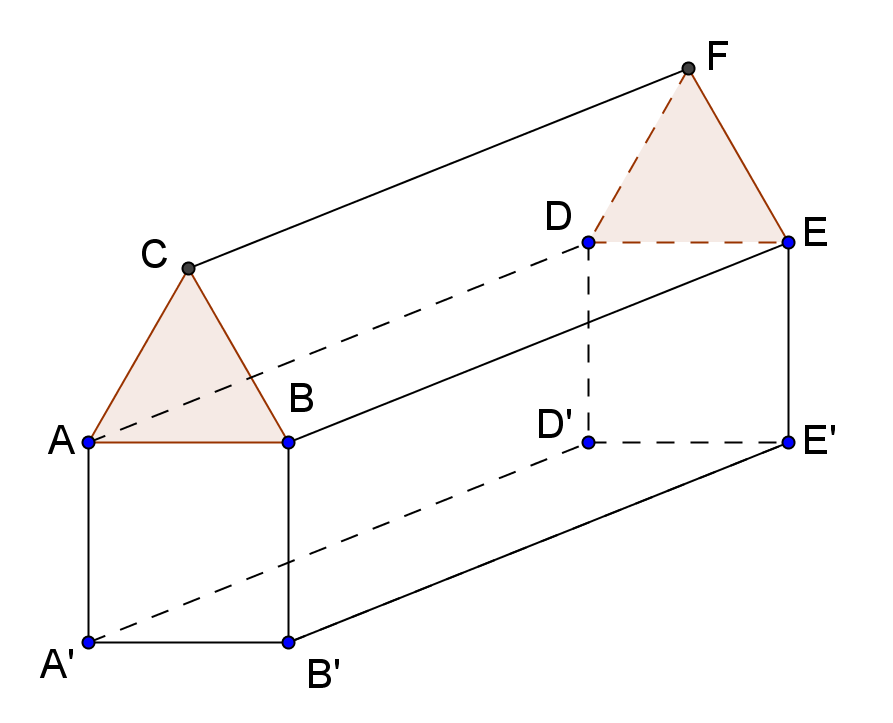
1. Un cort este format dintr-o prismă triunghiulară regulată ABCDEF şi un paralelipiped dreptunghic ABEDA’B’E’D’, ca în Figura 2. Se cunoaşte volumul cortului de \(12+3\sqrt{3}\)m³ şi AA’ = AB = 2 m.

 (5p)  a) Arătaţi că AD are lungimea de 3 m.

 (5p)  b) Aflaţi câţi m² de pânză s-au folosit pentru confecţionarea cortului? Aproximaţi prin adaos la întreg.

 (5p)  c) Determinaţi sinusul unghiului format de dreptele DC şi AE.

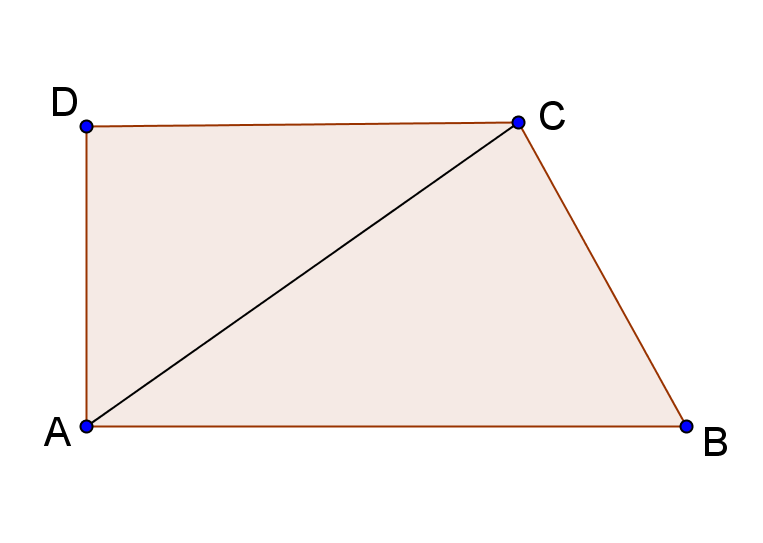
2. O grădină are forma unui trapez dreptunghic, ca în Figura 3. Se ştie că \(AB\parallel CD\), \(m\left( \sphericalangle A \right)=m\left( \sphericalangle D \right)={{90}^{0}}\), \(AC\bot BC\), \(AB=50\,m\) şi \(BC=40\,m\).

(5p)  a) Arătaţi că \(AC=30\,m\).

(5p)  b) Grădina se împrejmuieşte cu un gard format din 5 rânduri de sârmă. Aflaţi câţi metri de sârmă sunt necesari.

(5p)  c) Suprafaţa ADC este ocupată cu legume, iar suprafaţa ABC cu pomi fructiferi. Arătaţi că cele două suprafeţe sunt asemenea şi determinaţi raportul ariilor lor.