Varianta 71
Prof: Dima Paraschiva
- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.
- Timpul efectiv de lucru: 2 ore.
SUBIECTUL I – Pe foaia de examen se trec doar rezultatele. ( 30 de puncte)
(5p) 1. Rezultatul calculului 6+24:3=……………………..
(5p) 2. Numărul natural care este soluţie a ecuaţiei x + 3 = 5 este ………..
(5p) 3. Numărul 1,(6) transformat în fracţie ordinară este egal cu ………
(5p) 4. Un cub are lungimea muchiei egală cu 10 cm. Aria totală a cubului este egală cu .... cm2.
(5p) 5 Aria laterală a unei piramide patrulatere regulate cu muchia bazei de 6 cm şi înălţimea de \(3\sqrt{3}\)cm este egală cu …………cm2.
(5p) 6. La un concurs elevii au obţinut rezultatele conform tabelului de mai jos:
Mai mult de 8p au obţinut un număr de ........elevi.
SUBIECTUL II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)
(5p) 1. Desenaţi un cub ABCDA’B’C’D’.
(5p) 2. Rezolvaţi ecuaţia \(\frac{\text{x+2}}{\text{2}}-\frac{x}{3}=\frac{2x+3}{6}\).
(5p) 3. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R},f(x)=2x-1\) Aflaţi numărul a astfel încât A(a,5) aparţine reprezentării grafice a funcţiei f.
4. Ana are un număr de timbre poş Dacă le-ar împăţi în grupe de câte 4, 5, respectiv 6 timbre i-ar rămâne de fiecare dată două timbre negrupate.
(5p) a) Poate avea Ana 242 de timbre poştale ?
(5p) b) Care este cel mai mic numar de timbre pe care-l poate avea Ana ştiind că acest număr este mai mare decât 10 ?
(5p) 5. Să se determine necunoscutele x şi y din ecuaţia \(\sqrt{{{\left( 2x-4 \right)}^{2}}}+{{\left( 3x+2y-8 \right)}^{2}}=0\)
SUBIECTUL III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)
|
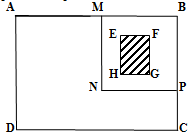
1. Dreptunghiul ABCD reprezintă suprafaţa unei microferme , iar dreptunghiul EFGH reprezintă suprafaţa unui grajd. EH = 30 m , EF = 20 m, AD = 64 m , AB = 100 m . Pătratul MNPB reprezintă uţarc cu MN = x metri . |
|
Exprimaţi în funcţie de x , suprafaţa ţarcului fără grajdul de pe el |
|
Care este valoarea lui x , dacă suprafaţa ţarcului (fără grajd ) este un sfert din suprafaţa întregului teren ? |
|
Calculaţi suprafaţa poligonului AMNPCD respectând condiţia de la punctul b) |
|
Dacă terenul AMNPCD este cultivat cu sfeclă furajeră , iar producţia la hectar este în medie de 50 de tone , aflaţi ce cantitate de sfeclă poate fi abţinută (Aproximaţi în tone recota scontată ). |
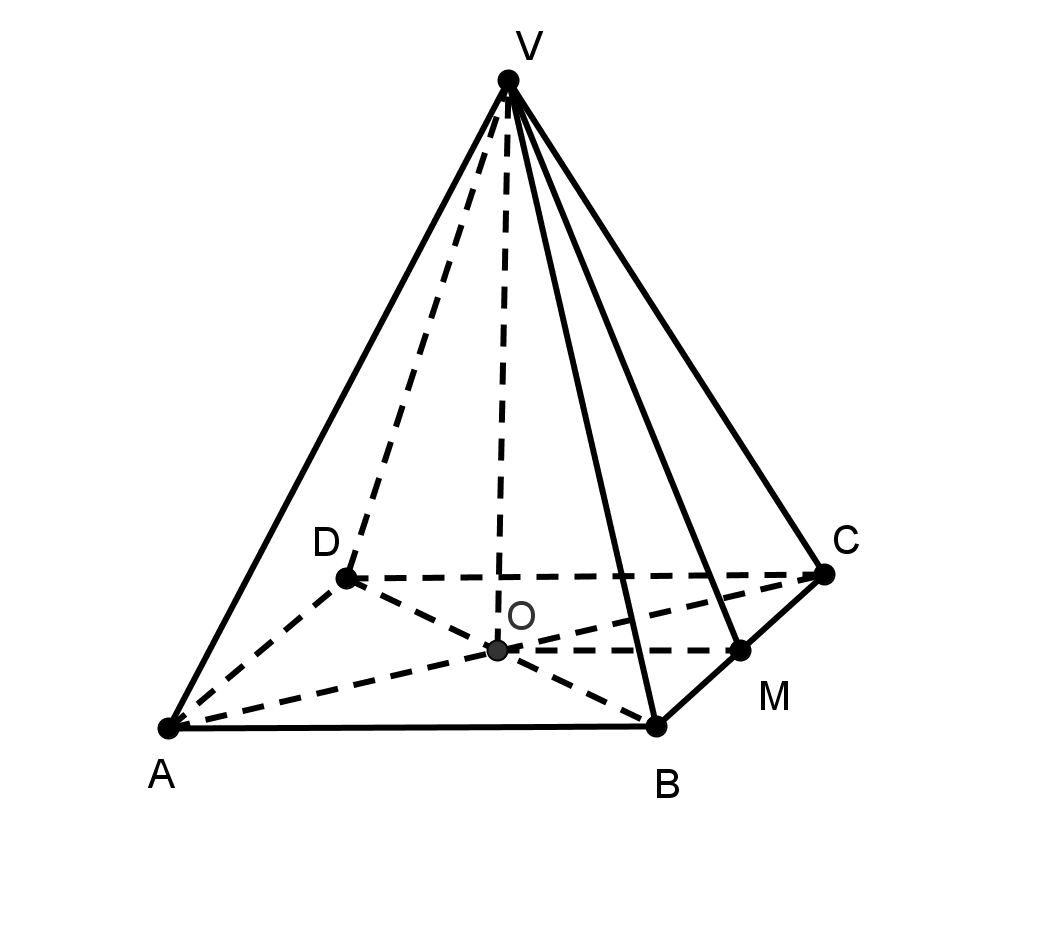
- În figura 2. VABCD are formă de piramidă patrulateră regulată cu latura bazei de 6 dm, înălţimea de 4 dm şi este din ciocolată.
(5p) a) Calculaţi volumul piramidei VABCD.
(5p) b) Piesa este topită şi tranformată în tablete în formă de paralelipiped dreptunghic cu laturile de 5 cm, 3 cm şi respectiv 2 cm. Câte astfel de tablete se obţin?
(5p) c)Tabletele sunt ambalate în cutii de cate 100 bucăţi, apoi acestea sunt aşezate in cutii mai mari în care încap maxim 10 cutii mici. Care este numărul minim de cutii mari necesare?