Varianta 72

Prof: Dobre Andrei Octavian

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Daca |-2x-6|=0 atunci numărul x este ...

(5p)     2. Dan doreşte să cumpere o carte cu banii stranşi în puşculiţă. El are 100 de monede de 10 bani, 30 de monede de 50 de bani şi 10 bancnote de 1 leu.

Dacă o carte costă 25 lei lui Dan îi rămân ... lei

(5p)     3. După o reducere de 10% un laptop costă 2430 lei. Preţul iniţial al laptopului a fost de .....lei

(5p)     4. Într-un triunghi oarecare baza este \(\frac{1}{3}\)din dublul înălţimii. Dacă baza triunghiului este 6 cm atunci aria triunghiului este ....cm²

(5p)     5. Într-un vas în formă de cub cu latura de 1 m încap ... litri de apă.

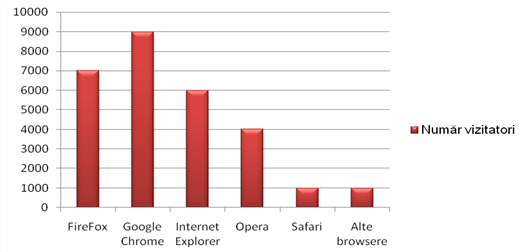
(5p)     6. În graficul de mai jos putem vedea ce browsere folosesc vizitatorii site-ului www.mateinfo.ro . FireFox este folosit de ...% din vizitatori.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenati cubul MATEINFO si realizaţi desfăşurarea plană a acestuia.

(5p)     2. Fie mulţimea \(\begin{align}  & A=\{x\in \mathbb{R}/|2x-4|+|x-2|\le 0\} \\ & B=\{x\in \mathbb{R}/|x-2|\le 2\} \\ \end{align}\) Enumeraţi elementele mulţimii A\(\cap \)B

(5p)     3. Numărul vizitatorilor site-ului www.mateinfo.ro din ultima luna a fost de 9000. Dintre aceştia 0,(3) sunt profesori, 25% sunt părinţi iar restul elevi. Câti elevi au vizitat site-ul în ultima lună?

 4. Fie functia f\(:\mathbb{R}\to \mathbb{R}\), f(x) = (a-2)x+1

(5p)    a) Determinaţi valorile lui a pentru care punctul A(a,16)\(\in \)G_f

(5p)    b) Daca a = 5 aflati distanţa de la punctul C(0,-3) la graficul funcţiei f

(5p)     5. Determinaţi mulţimea \(A=\{x\in \mathbb{N}/\frac{\sqrt{{{(3-2\sqrt{3})}^{2}}}+{{(1-\sqrt{3})}^{2}}+(\sqrt{3}-1)(\sqrt{3}+1)}{x+2}\in \mathbb{Z}\}\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Piramida lui Keops este o piramidă patrulateră regulată construită din 1 200 000 de blocuri de calcar cu greutăţi între 2,5 şi 15 tone. Piramida este înaltă de 138 m  iar unghiul dintre o muchie laterală şi planul bazei este de 60⁰

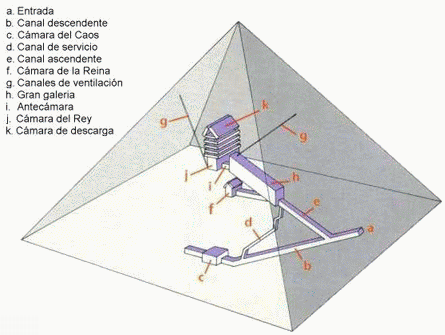
 (5p)  a) Dacă pentru construcţia ei s-au pus lunar 3000 de blocuri de calcar pana la finalizarea ei, iar construcţia a început pe 5 februarie, în ce lună fost finalizată piramida?

 (5p)  b) Aflaţi la ce distanţă faţă de vârful piramidei este camera mortuară a faraonului care se află chiar în „inima piramidei” fiind la distanţă egală de vârfurile piramidei.

 (5p)  c) Aflaţi volumul de calcar cunoscând faptul că în piramidă sunt tunele şi spaţii cu un volum de 4016 m³

2. Un elev masoară distanţa de la baza unui pom notată cu A şi baza blocului său notată cu B şi observă că este de 30 m, iar distanţa din acelaşi punct A la un pom notat cu MN este \(10\sqrt{3}\)m . Cu un aparat special cu laser stabileşte că măsura unghiului dintre planul pamântului şi dreapta AC este de 30⁰ şi că punctele C, M, A sunt coliniare.

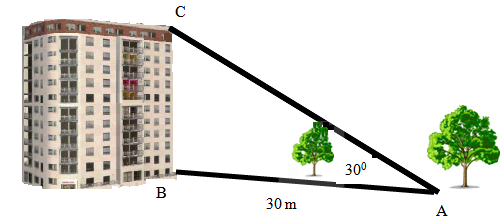
 (5p)  a) Aflaţi înălţimea blocului

(5p)  b) Ştiind că parterul are 3 m şi fiecare etaj al blocului are 2,5m aflaţi până la ce etaj este pomul notat cu MN daca  BB₁ este parter, B₁ B₂ etajul 1, B₂ B₃ etajul 2 şi aşa mai departe. 

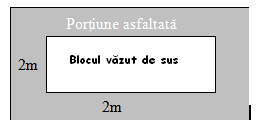
(5p)  c) Baza blocului este un dreptunghi cu lungimea de 20 m şi lătimea de 10m.

Dacă se asfalteza o alee de 2 m în jurul blocului, aflaţi aria suprafeţei asfaltate.