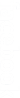Varianta 74

Prof:Dobre Andrei Octavian

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Ecuatia \({{(x+2)}^{2}}-(x+2)(x-2)=0\) are soluţia …

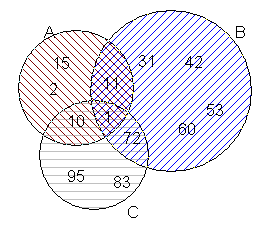
(5p)     2. Mulţimea\((A\cap B)\backslash C\)este {...}

(5p)     3. Un om de zăpadă are 10 kg. El se topeşte cu 0,2% pe minut. Masa lui după doua minute este de ... kg

(5p)     4. O sârma are lungimea de 2\(\pi \). Daca îndoim sârmă în  jurul unui obiect în formă de cerc obţinem un disc cu aria de ...

(5p)     5. Un bazin are lungimea de 8 m, lăţimea de 2 m iar înălţimea este media geometrică dintre lungime şi lăţime. Atunci în bazin intră ... litri de apă

(5p)     6. Dacă în ultima săptamână pe www.mateinfo.ro au intrat 4000 de vizitatori din străinatate, conform graficului de mai jos numărul vizitatorilor din Moldova este ...

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen o piramidă VMATE şi secţionaţi-o cu un plan (INFO) paralel cu baza  după care scrieţi denumirea trunchiului de piramidă obţinut.

(5p)     2. Dacă \(A=\{x\in \mathbb{Z}/\frac{2x-4}{x+1}\in Z\}\), enumeraţi elementele mulţimii\(A\cap N\).

(5p)     3. Media aritmetică a zece numere este 20. Daca media aritmetică a primelor opt numere este doi  aflaţi media aritmetica a ultimelor doua numere.

4. Fie funcţiile: \(\begin{align} & f:\mathbb{R}\to \mathbb{R},f(x)=-2x+6 \\ & g:\mathbb{R}\to \mathbb{R},g(x)=x-3 \\ \end{align}\)

(5p)    a) Determinaţi coordonatele punctului de intersecţie al graficelor celor doua funcţii

(5p)    b) Calculaţi aria suprafeţei cuprinsă între axa Oy şi graficele funcţiilor f şi g

(5p)     5. Arătaţi că numărul a=\((\sqrt{5}+2)\cdot \sqrt{9-4\sqrt{5}}+{{(\sqrt{2}+2)}^{2}}(6-4\sqrt{2})\in \mathbb{N}\)               

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un lingou de aur în formă de paralelipiped dreptunghic are lungime de 20 cm, lătimea de 10 cm şi înălţimea de 15 cm.

 (5p)  a) Calculaţi ce valoare are un lingou de aur dacă 1 cm³ costa 200 €.

 (5p)  b) Din acest lingou se doreşte realizarea unor zaruri cu latura de 5 cm. Câte zaruri vom obţine?

 (5p)  c) La un moment dat unul din zarurile de la b) se doreşte a fi transformat într-o bijuterie în formă piramidă patrulateră regulată de volum maxim astfel încât să se piardă cât mai puţin aur (zarul nu va fi topit ci taiat).Care este aria totală a piramidei?

2. În desenul de mai jos avem reprezentată zona din jurul unui coş de baschet cu dimensiunile aferente.

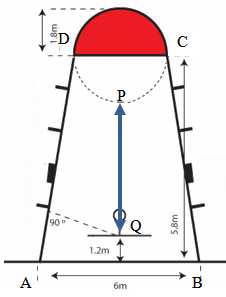
(5p)  a) Aflaţi aria semicercului haşurat cu rosu

(5p)  b) Aflaţi aria trapezului ABCD

(5p)  c) Urmărind datele din desenul de mai sus aflaţi PQ