Varianta 108

Prof: Mişca Maria

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Soluţia ecuaţiei  5 + x  = 15 ,  este egală cu ........

(5p)     2. Dintre numerele 3, (4) si 3,4 mai mare este numărul............

(5p)     3. Media geometrică a numerelor  4 şi 25 este egală cu ...............

(5p)     4. Suma lungimilor muchiilor unui cub este de 96 cm.Lungimea muchiei cubului este ..........cm

(5p)     5. Diagonala unui pătrat cu latura de 8 cm are lungimea de…………cm.

(5p)     6.O prismă patrulateră regulată dreaptă are aria laterală 480 cm²  si  înălţimea de 6 cm. Latura bazei prismei are lungimea de..........cm

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un paralelipiped dreptunghic  ABCDA^٠B^٠C^٠D^٠.

(5p)     2. Într-o şcoală sunt 420 de elevi, 40%  dintre ei participă la olimpiade şi concursuri pe discipline. Câţi  elevi participă la olimpiade şi concursuri pe discipline?

(5p)    3. Rezolvaţi  în R  ecuaţia: \(\frac{5(x+3)}{6}+2\frac{3}{4}=\frac{3x+2}{3}-\frac{3-x}{2}\)   

4.Fie funcţia f: R→ R ,  f(x) = 2x-1.

(5p)      a)  Reprezentaţi grafic funcţia f într-un sistem de axe ortogonale xOy.

(5p)      b) Arătaţi că numărul n = f(1) + f(2) + f(3) + ... + f(2007) este pătrat perfect.

 5. Fie expresia: E(x) = (\(\frac{x}{x-2}\) + \(\frac{x-2}{x}\) - 1) :\(\frac{{{x}^{2}}-2x+4}{x}\) , x \(\in \)R - { 0, 2 } Arătaţi că E(x) =  \(\frac{1}{x-2}\),  pentru orice x \(\in \)R - { 0, 2 } 

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

1. Pe planul pătratului ABCD, cu lungimea laturii de 6 cm, se ridică perpendiculara AM,AM = 6cm.

 (5p)  a) Demonstraţi că triunghiul MBD este echilateral

 (5p)  b) Calculati distanţa de la M la BD.            

 (5p)  c) Aflaţi sinusul unghiului format de dreapta MC cu planul (ABC).

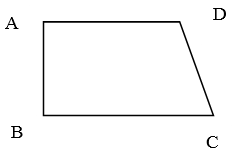
 2. În figura alăturată, ABCD este un trapez dreptunghic în A, având bazele (AD) şi respectiv (BC) de lungimi 12m şi 16 m şi măsura unghiului C de 60⁰.

(5p)  a) Determinaţi perimetrul trapezului.

(5p)  b) Dacă ABCD reprezintă suprafaţa unui salon, câţi metri pătraţi de parchet sunt necesari pentru parchetarea    întregului salon? (Se ia în calcul \(\sqrt{3}\)=1,7).       

(5p)  c) Dacă 1 metru pătrat de parchet costă 30 lei , verificaţi dacă 2900 lei sunt suficienţi pentru cumpărarea parchetului necesar parchetării salonului?