Varianta 140

Prof: Valer Pop

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului 72:4-12 este egal cu ...........

(5p)     2. Numărul natural care aparţine mulţimii \(\{\frac{3}{5};1,25;\sqrt{36};+\sqrt{8};-\sqrt{4};{{0,5}^{2}}\}\) este...........

(5p)     3. Media aritmetică a numerelor  23 şi 5 este egală cu ..............

(5p)     4. Linia mijlocie a unui triunghi echilateral cu perimetrul de 54 cm are lungimea egală      cu ...........cm.

(5p)     5. Cubul cu muchia de 4 cm are volumul egal cu ............cm³.

(5p)     6. La un concurs elevii au obţinut rezultatele conform tabelului de mai jos:

Mai mult de 6p au obţinut un număr de ........elevi.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen, un tetraedru VABC.

(5p)     2. Într-o şcoală învaţă la ciclul primar 186 de elevi iar la ciclul gimnazial cu 16 elevi         mai  mulţi decât \(\frac{29}{31}\)din numărul celor din ciclul primar. Câţi elevi învaţă în acea         şcoală ?            

(5p)     3. Se dă funcţia f:{1;2;3;5}→ [-1;7],  f(x)=2x-3. Verificaţi dacă punctele A(1;-1) şi          B(5;6) aparţin graficului funcţiei f.

 4. Într-o cutie sunt mai mult de 60 de bomboane dar mai puţin de 69 de bomboane.

 (5p)    a). Câte bomboane sunt în cutie dacă împărţindu-le în mod egal la 13 copii mai               rămân două ?

(5p)    b). Dacă s-ar împărţi la 7 copii câte 6 bomboane şi la 6 copii câte 5 bomboane ar fi           de ajuns ?

(5p)     5. Arătaţi că  \(\text{E}\left( \text{x} \right)={{\left( \text{x}+\text{3} \right)}^{\text{2}}}-{{\left( \text{2x}-\text{1} \right)}^{\text{2}}}+\text{3x}\left( \text{x}-\text{3} \right)+\text{1}-\text{x}\) este număr natural pentru orice x real.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

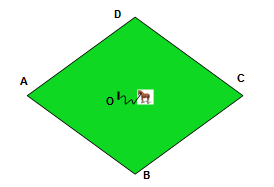
1. În figura de mai jos este schiţa unui teren cu iarbă, în formă de romb, unde AC=48m şi BD=36m. Pe acest teren este legat un cal, cu un lanţ lung de 9m, de un          ţăruş fixat în punctul O.

 (5p)  a) Calculaţi aria şi perimetrul terenului.

 (5p)  b) Calculaţi aria suprafeţei maxime pe care o poate paşte calul.

 (5p)  c) Arătaţi că acel cal nu poate paşte mai mult de 30% din suprafaţa terenului.

 2. Un rezervor pentru apă are formă de paralelipiped dreptunghic cu diagonala bazei de 3m şi dimensiunile direct proporţionale cu 4, 3 şi 2. Cea mai mică dintre dimensiuni      este înălţimea.

(5p)  a) Calculaţi dimensiunile rezervorului.

(5p)  b) Dacă  rezervorul gol are masa de 516 kg, calculaţi masa rezervorului plin cu apă.

(5p)  c) Calculaţi suprafaţa de teren care poate fi udată în medie cu 8 litri de apă pe metru          pătrat             folosind 75% din capacitatea rezervorului.