Varianta 136

Prof: Valer Pop

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Dintre numerele \(2\sqrt{3}\) şi \(3\sqrt{2}\) mai mare este ……….

(5p)     2. Cifra unităţilor numărului 987⁴ este ………

(5p)     3 Rezultatul calculului \(5a+a-6a\)este egal cu ……….

(5p)     4. Rombul care are perimetrul de 48 cm are lungimea laturii de …….. cm.

(5p)     5. Aria totală a unui tetraedru regulat este de 200 cm². Cât este aria bazei ?

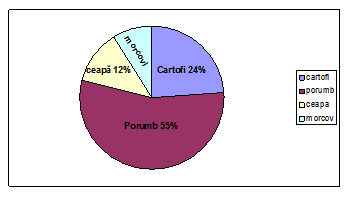
(5p)     6. Un teren este cultivat cu porumb, cartofi, ceapă şi morcovi aşa cum arată figura de      mai jos. Cât la sută din suprafaţa terenului s-a cultivat cu morcovi ?

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi un paralelogram ABCD, unde \(m(\sphericalangle A)>{{90}^{0}}\).

(5p)   2. Un televizor costă 640 de lei şi o maşină de spălat costă de două ori mai mult. Dacă    televizorul se ieftineşte cu 15% iar maşina de spălat se scumpeşte cu 5%, calculaţi cât    vor costa împreună cele două obiecte.

(5p)     3. Calculaţi  \(|2\sqrt{3}-3|+|1-\sqrt{3}|-(\sqrt{3}+2)+6-\sqrt{12}\)

 4. Elevii unei şcoli vor purta uniforme. Pentru 5 uniforme de fete şi 8 uniforme de băieţi   sunt necesari 34 m de stofă iar pentru 9 uniforme de fete şi 6 de băieţi, 36m de           stofă.

(5p)    a) Câţi metri de stofă sunt necesari pentru confecţionarea unei uniforme de băiat?

(5p)    b) Câte uniforme se pot confecţiona din 11 m de stofă?

(5p)     5. Se dă funcţia \(f:\mathbb{R}\to \mathbb{R},\)\(f(x)=-x+6\). Determinaţi coordonatele punctului M de        pe graficul funcţiei care are ordonata cât dublul abscisei.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

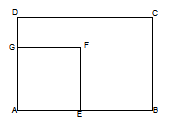
1. Un teren arată ca în figura de mai jos, unde ABCD este dreptunghi iar AEFG este pătrat. Se dă AB=48m, BC=36m iar AE=x

 (5p)  a) ) Să se exprime aria porţiunii EBCDGF  în funcţie de x.

(5p)  b) Să se calculeze x dacă aria pătratului AEFG este jumătate din aria poligonului    EBCDGF.

 (5p)  c) Porţiunea de teren AEFG cu latura determinată la punctul b) se vinde cu 1200 Euro pentru un ar. Câţi lei încasează vânzătorul terenului dacă un Euro se schimbă cu 4,20 lei ?

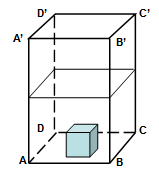
2. Un vas în formă de prismă patrulateră regulată ABCDA’B’C’D’ , ca în figura de mai jos, are latura bazei de 40 cm. Vasul este umplut cu apă până la jumătatea înălţimii sale.

(5p)  a) Ce înălţime are vasul dacă are o capacitate de 96 de litri?

 (5p)  b) Ce lungime are muchia unui cub, care dacă se scufundă în apa din vas face ca nivelul apei să se ridice cu 5 cm ?

 (5p)  c) Calculaţi raportul dintre aria laterală a vasului şi aria totală a cubului.