Varianta 142

Prof: Raţ Cristina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(3(-5)+5\cdot 1,2+9\) este.....

(5p)     2. Cel mai mare divizor comun dintre 12 si 15 este.....

(5p)     3. Soluţia reala a ecuaţiei 3x+2=5 este.....

(5p)     4. Ipotenuza triunghiul dreptunghic ABC cu catetele de 12 cm, respectiv 16 cm este.....

(5p)     5. Volumul cubului cu latura de 6 cm este.....

(5p)     6. Elevii unei clase au obţinut la matematică mediile din tabelul urmator.

                        Aflaţi media clasei.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi un cub ABCDMNPQ.

(5p)     2. Determinaţi numerele a,b,c \(\in \)R direct proporţionale cu 2,3,4 astfel încat \({{a}^{2}}+{{b}^{2}}+{{c}^{2}}=261\).

(5p)     3. Aflaţi x,y \(\in \mathbb{Z}\)dacă  ele verifică ecuaţiile 2x+3y=8 si 4x-y=2.

 4. Fie funcţia \(f:R\to R\),\(f(x)=ax+b\), a şi b \(\in \)R ştiind că f(1)=6 si punctul B(0,4) aparţine graficului funcţiei.

(5p)    a) Aflaţi funcţia f(x).

(5p)    b) Dacă a=2 si b=4 aflaţi soluţia ecuaţiei f(x)=8.

(5p)     5. Calculaţi 20% din suma numerelor x=4,6+3,4 şi \(y=\frac{2}{3}+\frac{5}{4}+\frac{1}{12}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Pentru acoperişul unei case in formă de piramidă patrulateră regulată cu muchia bazei de 8 cm şi înalţimea de 3 cm se foloseşte tablă roşie , iar muchiile se construiesc din lemn.

 (5p)  a) Aflaţi dacă 60 m de lemn sunt suficienţi pentru muchiile piramidei.

 (5p)  b) De câţi metrii pătraţi de tablă are nevoie construcţia?

 (5p)  c) Dacă preţul unui metru pătrat de tablă este de 2 ori mai mare decât un metru liniar de lemn şi preţul lucrării a fost 2200 lei, aflaţi cât costă un metru pătrat de tablă şi un metru liniar de lemn.

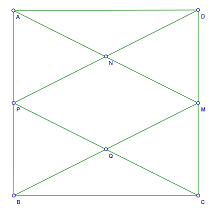
 2. Pentru amenajarea unei bucătării în formă de pătrat cu latura de 8 cm, se foloseşte parchet şi gresie. Suprafaţa acoperită de gresie este delimitată de 4 drepte formate de vârfuri cu mijlocul unei laturi AM,BM,DP,CP, unde M\(\in \)(DC) şi P\(\in \)(AB).

(5p)  a) Aflaţi aria suprafeţei acoperită cu gresie.

(5p)  b) Pentru suprafaţa unde se pune parchet se cumpară pachete de câte 2 m\(^{2}\)la preţul de 75 lei pachetul. Cât costă tot parchetul, neglijând pierderile.

(5p)  c) Dacă echipa care lucrează este platită pentru montarea 1 m\(^{2}\) de gresie cu preţul de 25 lei şi pentru 1 m\(^{2}\)de parchet cu 15 lei , aflaţi costul manoperei.