Varianta 151

Prof.  Ştefan Maria Lăcrămioara

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Dacă \(\frac{2\sqrt{3}}{x}=\frac{9}{\sqrt{243}}\), atunci numărul x este egal cu ………

(5p)     2. Un produs electrocasnic costă 1375 lei. După o reducere de 8% acelaşi obiect va costa ……………..lei .

(5p)     3. În data de 31 decembrie 2010 la ora 20 temperatura aerului este de 2⁰C. În următoarele ore temperatura scade câte 2 grade la fiecare oră. După 4 ore temperatura va fi de  ……….⁰C.

(5p)     4. Aria unui pătrat cu diagonala de \(3\sqrt{6}cm\) este de ……cm².

(5p)     5. Se considera piramida patrulateră regulată [VABCD] din figura 1, astfel încât triunghiul VAC este dreptunghic. Măsura unghiului format de muchia VA cu planul bazei este de ………⁰.

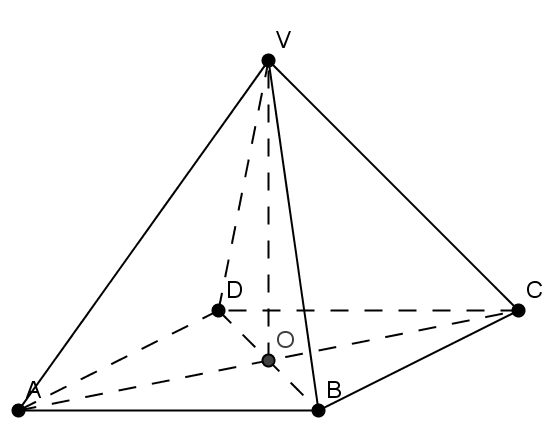 Figura 1

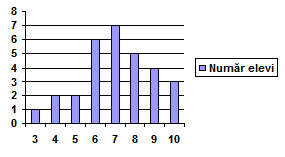
(5p)     6. În graficul următor este reprezentat rezultatul obţinut de  elevii clasei a VIII-a la un test de matematică. Numărul elevilor care au promovat testul este ………..

        SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de lucrare, o prismă triunghiulară ABCA’B’C’.

(5p)     2. Determinaţi mulţimea \(A=\left\{ x\in \mathbb{Z}|\frac{3x+1}{2x-5}\in \mathbb{Z} \right\}\).

(5p)     3. Un elev citeşte \(\frac{3}{7}\)dintr-o carte şi constată că mai are 5 pagini până la jumătate. Câte pagini are cartea?

 4. Se consideră expresia \(E\left( x \right)=\left( \frac{x+1}{x+2}-\frac{4}{{{x}^{2}}-4}-\frac{6}{2-x} \right)\cdot {{\left( \frac{x+3}{2{{x}^{2}}-5x+2} \right)}^{-1}}\), unde \(x\in \mathbb{R}\backslash \left\{ -3;-2;\frac{1}{2};2 \right\}.\)

(5p)    a) Arătaţi că forma cea mai simplă a expresiei este \(E\left( x \right)=2x-1\).

(5p)    b) Determinaţi valorile reale ale lui \(x\) pentru care \(E\left( x \right)+3\sqrt{5}=\frac{4}{E\left( x \right)-3\sqrt{5}}.\)

(5p)     5. Se consideră numerele \(a=\left( 7-4\sqrt{3} \right)\left( 3+\sqrt{5} \right)\) şi \(b=\left( 7+4\sqrt{3} \right)\left( 3-\sqrt{5} \right)\). Calculaţi media geometrică a celor două numere.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

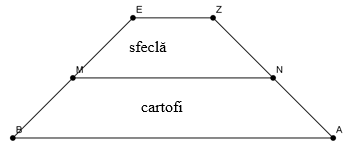
1. Fie un teren în formă de trapez BAZE isoscel, AB || ZE, \(m\left( \sphericalangle A \right)={{45}^{0}}\), ZE = 40 m, MN este linie mijlocie şi lungimea înălţimii trapezului este de 60 m. Terenul se cultivă cu sfeclă şi cartofi, după cum se vede în figura alăturată

 (5p)  a) Calculaţi lungimea gardului care separă cele două culturi pe linia mijlocie.

 (5p)  b) Calculaţi suprafaţa cultivată cu sfeclă, respectiv cu cartofi.

 (5p)  c) Calculaţi cât la sută din suprafaţa cultivată cu cartofi, reprezintă suprafaţa cultivată cu sfeclă.

2. În figura 2 este reprezentat un bazin în formă de paralelipiped dreptunghic, cu dimensiunile L = 24 m, l = 3 m şi adâncimea h = 2,4 m. Pentru placarea cu faianţă se folosesc plăci în formă de pătrate cu dimensiunea de 30 cm şi colţare în formă de baghete de 0,6 m lungime.

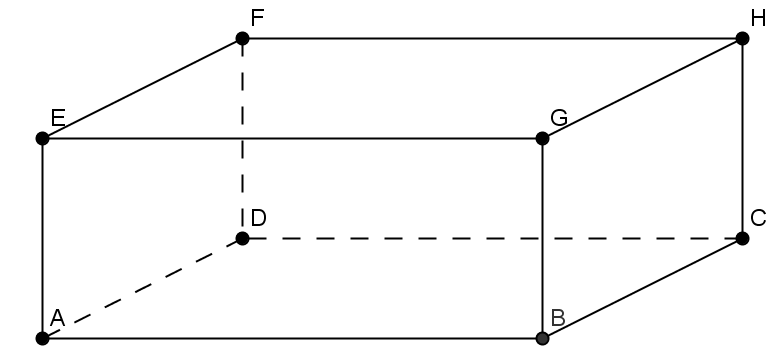
 Figura 2

 (5p)  a) Arătaţi că bazinul se poate acoperi cu plăci întregi de faianţă.

 (5p)  b) Calculaţi suprafaţa acoperită cu faianţă

 (5p)  c) Se achiziţionează faianţa în cutii care conţin 50 de plăci pentru placare şi se cumpără în plus cu 5% din suprafaţă pentru rezervă. Ştiind că se vând doar cutii întregi (nu se vinde faianţa la bucată) calculaţi câte cutii sunt necesare.