Varianta 154

Prof.  Ştefan Maria Lăcrămioara

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(24{{x}^{3}}:\left( 2x+x+3x \right)\) este egal cu……….

(5p)     2. 100 g soluţie salină cu concentraţia 2% conţine ………. g sare

(5p)     3. Valoarea de adevăr a propoziţiei \({{\left( x+2 \right)}^{2}}={{x}^{2}}+4\) este ……….

(5p)     4. Latura unui pătrat cu aria \(24\)\(c{{m}^{2}}\) este ... cm.

(5p)     5. Se consideră piramida patrulateră regulată \(VABCD\) din Figura 1, având \(AB=6\)cm şi \(VA=6\sqrt{2}\)cm. Măsura unghiului dintre dreptele \(VB\) şi \(VD\) este egală cu …..\({}^\circ \)

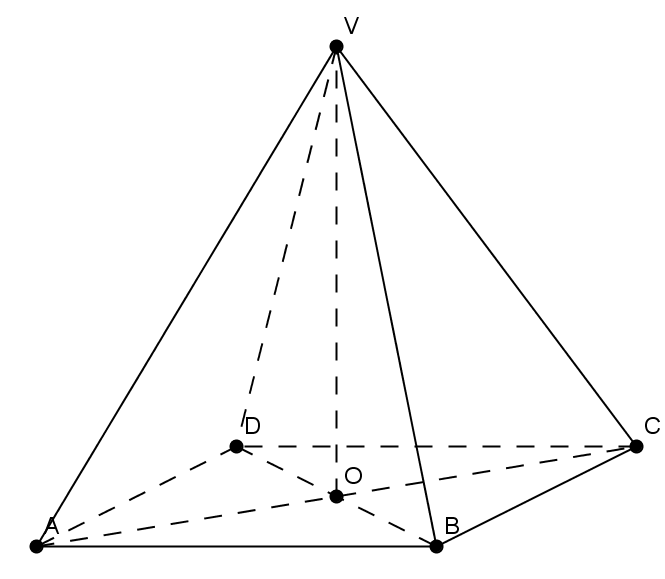
Figura 1    

(5p)     6. În tabelul de mai jos sunt reprezentate rezultatele obţinute de toţi elevii clasei a VIII-a la examenul de matematică. Procentul de promovabilitate este … %

           SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen un cub \(ABCDA'B'C'D'\).

(5p)     2. Se consideră mulţimea \(A=\left\{ -\frac{\sqrt{270}}{\sqrt{30}};\sqrt{1+{{\left( \frac{3}{4} \right)}^{2}}};\sqrt{80};\sqrt{{{26}^{2}}-{{10}^{2}}};\sqrt{{{4}^{3}}};\sqrt{1+{{\left( \frac{2}{5} \right)}^{2}}} \right\}\). Enumeraţi elementele \(A\cap \mathbb{Q}\).

(5p)     3. Fie funcţia \(f:\mathbb{R}\to \mathbb{R};\)\(f\left( x \right)=3x-5\). Determinaţi numărul real \(a\) pentru care punctul \(P\left( a;1 \right)\) este situat pe graficul funcţiei \(f\).

 4. Un bloc are 19 apartamente cu 2 şi 4 camere, în total 48 camere. Aflaţi:

(5p)    a) numărul apartamentelor cu 4 camere.

(5p)    b) numărul apartamentelor cu 2 camere.

(5p)     5. Fie expresia \(E\left( x \right)=\sqrt{{{x}^{2}}+6x+13}+\sqrt{{{y}^{2}}-10y+34}\). Arătaţi că \(E\left( x \right)\ge 5\) pentru orice \(x,y\in \mathbb{R}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Se consideră un rezervor în formă de paralelipiped dreptunghic cu lungimea dublul lăţimii şi înălţimea media aritmetică dintre lungime şi lăţime.

 (5p)  a) Determinaţi dimensiunile astfel încât în rezervor să încapă \(3t\) de apă.

 (5p)  b) Calculaţi în cât timp se va umple bazinul cu ajutorul unui robinet cu debitul de 120 l de apă pe minut.

 (5p)  c) Calculaţi înălţimea la care se va ridica apa în bazin după 9 minute.

 2. În Figura 2 este reprezentată schiţa unei plăci metalice din care se decupează două discuri cu raza \(R=40\)cm. Partea rămasă după decupare reprezintă deşeu ce se trimite la retopire. Cele două discuri sunt tangente între ele şi faţă de laturile dreptunghiului.

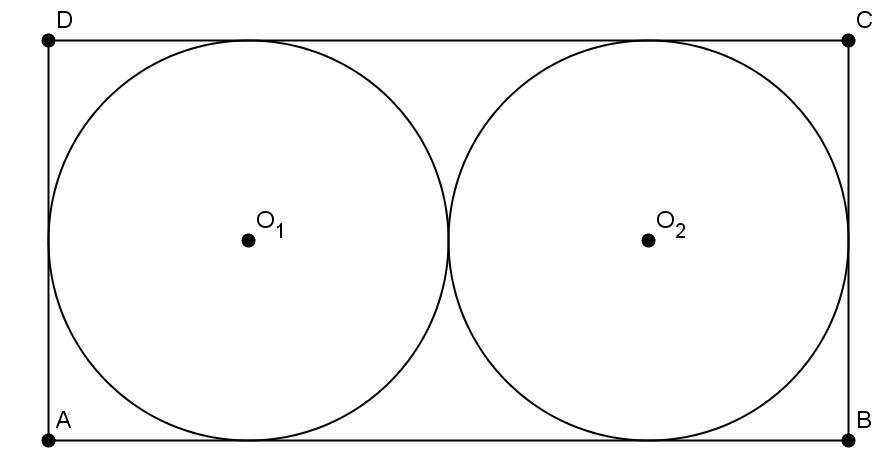
Figura 2

(5p)  a) Calculaţi aria celor două discuri.

(5p)  b) Calculaţi aria plăcii de metal.

(5p)  c) verificaţi dacă raportul dintre aria discului şi aria suprafeţei totale este mai mic decât 22% (se consideră \(3,14<x<3,15\))