Varianta 160

Prof. C. Telteu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Să se rezolve ecuaţia: \(x+\sqrt{3}-2\sqrt{3}+\sqrt{3}=0\)

(5p)     2. Media aritmetica a două numere este 12,5. Care este suma numerelor?

(5p)     3. Copii Adam, Barbu, Cătălina şi Doina se joacă pe un teren. Fetele s-au accidentat. Cât la sută din numărul copiilor de pe teren au rămas neaccidentaţi?

 (5p)     4. Un triunghi isoscel are o latură de 8 cm, şi altă latură de două ori mai mare ca aceasta. Care este perimetrul său?

(5p)     5. Un cort din pânză are forma de piramidă patrulateră regulată cu muchia laterală de naceeaşi lungime cu latura bazei, care este de 2 m. Care este suprafaţa de pânză necesară confecţionării lui, dacă presupunem că nu se pierde nimic în timpul confecţionării?

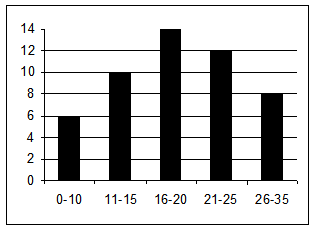
(5p)     6. În diagrama următoare, sunt date numărul de intrări pe messenger ale prietenilor lui Andrei, într-o lună.(orizontală - nr. intrări, verticală – nr. prieteni)

 Spunem că un prieten de pe listă este „vorbăreţ”  dacă are mai mult de 15 intrări. Câţi prieteni  „vorbăreţi” are Andrei?

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi un paralelipiped dreptunghic \(ABCDA'B'C'D'\) şi diagonalele feţelor ce conţin vârful  \(B\), iar \(B\) nu aparţine acestor diagonale.

(5p)     2. Dacă S este mulţimea soluţiilor ecuaţiei \(x-6=6\), iar \(P=\left\{ 10,11,12 \right\}\), atunci \(P\cap S=\)…

(5p)     3. Numerele 244, 99  şi 90 împărţite la un acelaşi număr natural \(n\), dau resturile 4, 3, respectiv 6. Care este cea mai mare valoare a lui\(n\)?

 4. Se dă funcţia: \(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=ax+3,\,\,\,\forall x\in \mathbb{R}\).

(5p)    a) Determinaţi numărul \(a\)  ştiind că graficul funcţiei trece prin punctul \(M\left( 1;3 \right)\)

(5p)    b) Determinaţi intersecţiile graficului cu  axele de coordonate, pentru \(a=1\).

(5p)     5. Verificaţi identitatea: \({{\left( x+1 \right)}^{2}}+{{\left( x-2 \right)}^{2}}+2\left( x+1 \right)\left( x-2 \right)-4x\left( x-1 \right)-1=0\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O hală dreptunghiulară se pardoseşte cu pietre în formă de pătrat cu latura de 15 cm. Hala este lungă de 32,5 m şi lată de 8,5 m. Între pietre nu rămâne loc liber, iar dacă dintr-o piatră se foloseşte o parte, restul nu se mai foloseşte.

 (5p)  a)Câte pietre sunt necesare?

 (5p)  b)Dacă piatra este groasă de 3 cm, ce volum de piatră s-a cumpărat?

 (5p)  c) Cât a costat piatra dacă un metru cub costă 1000 lei?

2. Un circ are formă de cerc cu raza de 25 m. Partea pe care se fac exerciţii (arena) este şi ea în formă de cerc cu raza de 20 m.

(5p)  a) Care este aria circului?

(5p)  b)Care este aria arenei?

(5p)  c) Să se afle câţi spectatori încap, dacă fiecare are nevoie de o suprafaţă de  0,5 m² ?