Varianta 162

Prof:C. Telteu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Găsiţi soluţia ecuaţiei: \(-7+x-x+8=3-x\)

(5p)     2. Pe o banchiză de gheaţă, sunt 250 de pinguini, iar pe o banchiză vecină cu 150 mai mulţi. Câţi pinguini sunt în total pe cele două banchize?

(5p)     3. Dacă din 24 de baloane, Irina a spart trei, cât la sută din numărul total de baloane au rămas nesparte?

(5p)     4. Un dreptunghi cu perimetrul de 30 cm, are lăţimea un sfert din lungime. Câţi cm are lăţimea sa?

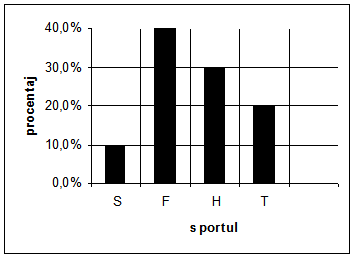
(5p)     5.  Cubul alăturat are muchia de 2 cm, iar M este mijlocul laturii. Calculaţi \({{A}_{MAC}}\).

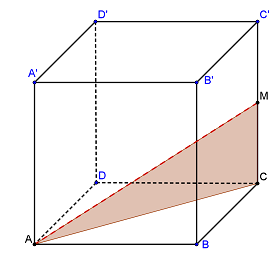
(5p)     6. Într-o şcoală, fiecare elev practică numai câte unul  din sporturile: şah, fotbal, handbal şi tenis. Diagrama următoare arată în procente   participarea lor la fiecare sport. Câţi elevi sunt în şcoală, dacă 50 de elevi practică şahul?

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o piramidă triunghiulară regulată, şi o apotemă a bazei.

(5p)     2. \({{D}_{5}}\)este mulţimea divizorilor lui  5; \(B\)este mulţimea cifrelor numerelor scrise în baza 10. \({{D}_{5}}\cap B=...\)

(5p)     3. Irina este de doua ori mai în vârstă decât cei doi fraţi ai ei, care sunt gemeni. Dacă toţi au împreună 12 ani, câţi ani are un frate al Irinei?

 4. Se dă funcţia: \(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=x-\frac{\sqrt{3}}{5},\forall x\in \mathbb{R}\).

(5p)    a) Determinaţi punctul de pe axa \(Ox\) ce aparţine graficului funcţiei

(5p)    b) Câte puncte ale graficului funcţiei au coordonatele numere întregi?

(5p)     5.  Calculaţi valoarea expresiei\(E\left( x \right)=\left( \frac{1}{x-\sqrt{2}}-\frac{1}{x+\sqrt{2}} \right)\cdot \frac{{{x}^{2}}-2}{2\sqrt{2}}-1\) pentru \(x=\frac{\sqrt{2}}{\sqrt{13}}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Pentru pavarea unei străzi se folosesc pietre paralelipipedice cu lungimea de 10 cm, lăţimea de 8 cm şi înălţimea de 6 cm.

 (5p)  a) Ce suprafaţă se poate pietrui cu 100000 pietre?

 (5p)  b) Dacă 1 m³ de piatră cântăreşte 3 t, Câte camioane au fost necesare pentru aducerea pietrei, dacă un camion transportă 15 t?

 (5p)  c) Dacă strada are lăţimea de 6 m, cât costă pavarea unui km de stradă, dacă la preţul pietrei (100 lei /tonă) se adaugă încă 10 % manoperă?

2. În trapezul \(ABCD,\,\,AB||\,CD,\,\,AB=40\,cm,\,\,BC=20\,\,cm,\,\) \(\,CD=15\,\,cm,\,\,AD=15\,\,cm,\,\,\) Fie \(AD\bigcap BC=\left\{ M \right\}\).

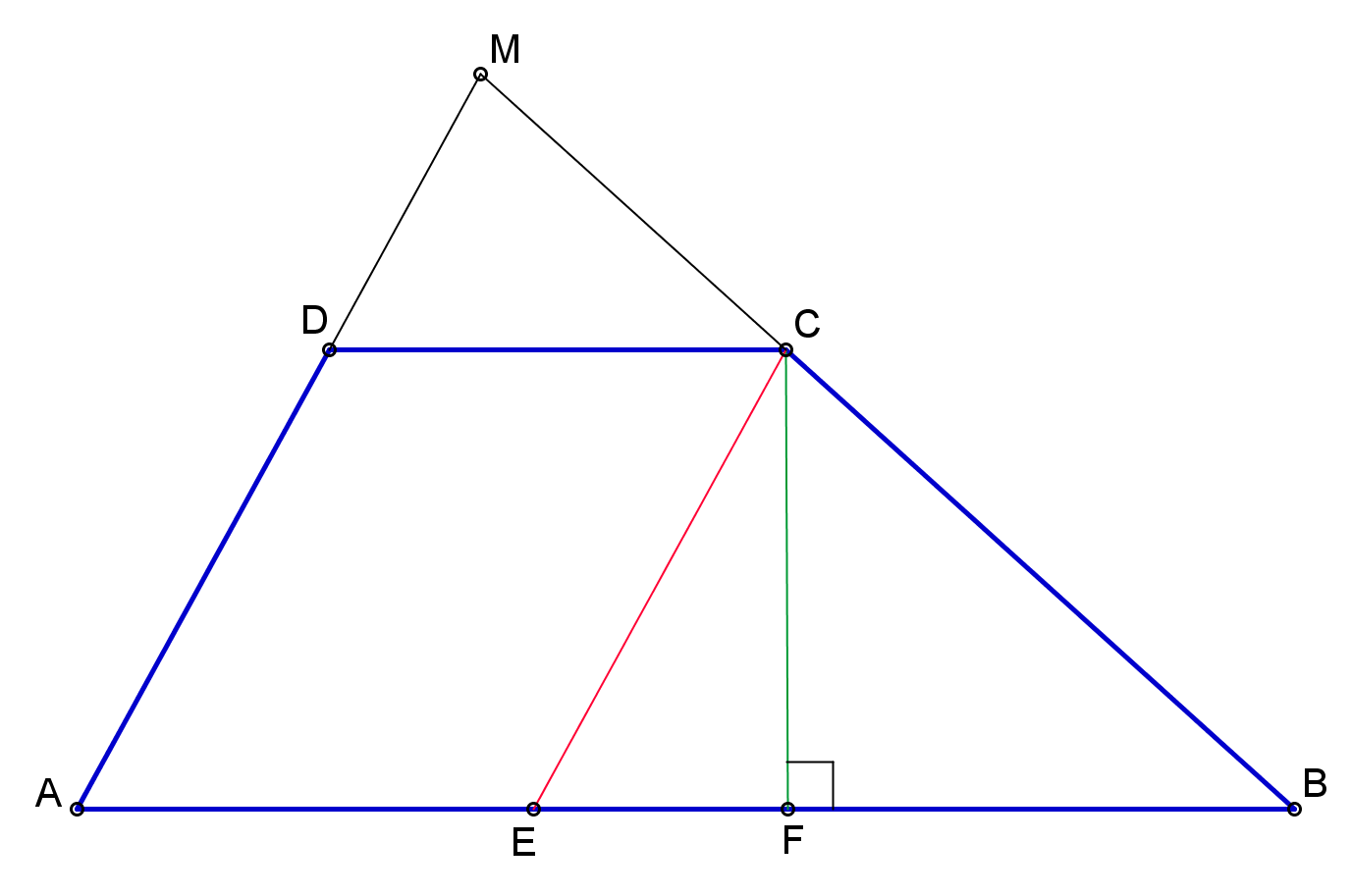
(5p)  a) Aflaţi aria trapezului .

(5p)  b) Aflaţi \({{P}_{MDC}}\).