Varianta 167

Prof: Vasile Uleanu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Calculând \((5\sqrt{3}+7\sqrt{3}):6\sqrt{3}\) se obţine…..

(5p)     2. Soluţia reală a ecuaţiei  \(-3\sqrt{2}x+6=3\) este …..

(5p)     3. Dacă x\(\in (-3,5]\)  ,  atunci numărul real 3 – 2x aparţine  intervalului…….

(5p)     4. Dacă a² – b² = 36 şi a + b =  18 , atunci  a –  b= …….

(5p)     5 Media geometrică a numerelor a= | \(4\sqrt{3}-7\)|    şi b = | 7 +\(4\sqrt{3}\)|\(\) este…..

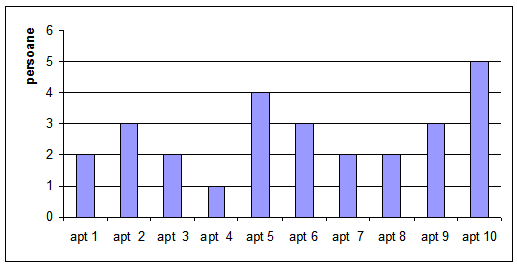
(5p)     6. Diagrama de mai jos reprezintă numărul de persoane  care locuiesc în apartamentele  de pe scara unui bloc. Numărul total de persoane din apartamentele notate cu număr impar este  de ……

  SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o piramidă patrulateră regulată VABCD cu baza ABCD.

        (5p)     2. Arătaţi că x este element al mulţimii A,  unde A={ 7³⁵  ,  81²⁷  , 4⁵⁴ }  şi x = [ 5·25¹²:125⁸ –  \(16\)⁴:\(2\mathop{^{2}}^{4}\) + (9²)⁷ : \({{^{{}}}^{{}}}{{3}^{{{3}^{3}}}}\)+ 49²: 7⁴] ³⁶                        

       (5p)     3. Calculaţi aria şi perimetrul unui triunghi dreptunghic, ştiind că mediana şi înălţimea corespunzătoare  ipotenuzei au lungimile de 5 cm, respectiv 4 cm .

4. Fie \(a=\frac{2}{1\cdot 3}+\frac{4}{3\cdot 7}+\frac{5}{7\cdot 12}+\frac{7}{12\cdot 19}\)

(5p)    a) Calculaţi valoarea numărului a.

(5p)    b) Arătaţi ca \(\)\(\frac{1}{3}<a<\frac{19}{20}\). \(\)

(5p)     5. Să se arate că A = \(\left[ (n-1)(n+1)\left( {{n}^{4}}+1 \right)\left( {{n}^{8}}+1 \right)+\frac{1}{{{n}^{2}}+1} \right]\left( {{n}^{4}}+{{n}^{2}} \right)\) este pătrat perfect.

 SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Un bazin de apă  în formă de paralelipiped dreptunghic cu L= 8m , l = 3m şi h= 2,5m este umplut  cu apă  până la  80% din volumul său .

 (5p)       a) Aflaţi câţi litri de apă sunt în bazin .

 (5p)       b) Dacă o familie consumă zilnic pentru nevoile casei  800 l de apă , aflaţi pentru  câte familii  ar putea sa ajungă apa din bazin intr-o zi dacă bazinul este  încărcat la capacitatea maximă .

 (5p)  c) Ştiind ca 1 m.c de apă costă 4,25 lei  , aflaţi cât a plătit  o familie pentru   consumul lunii noiembrie  2010 ,dacă consumul zilnic mediu este de  800 l apă.

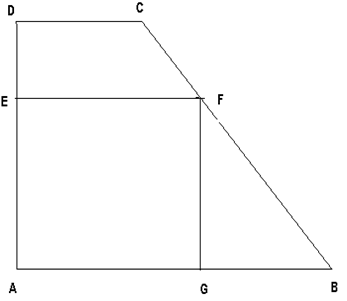
 2. Figura alăturată reprezintă schema un teren  agricol  în formă de trapez dreptunghic cu AB şi CD baze şi \(\prec \)A= 90 ⁰ , iar  AD= 30 m , DC = 10 m  Suprafaţa acestui teren a fost împărţită în trei parcele care au  de forma de  pătrat AGFE , trapez dreptunghic   DEFC şi triunghi dreptunghic isoscel FGB  .Dacă  aria trapezului DEFC este de 150 m²   , calculaţi:

(5p)  a) Suprafaţa terenului ABCD.

(5p)  b) Cât la % din aria pătratului AGFE reprezintă aria triunghiului BGF.