Varianta 168

Prof: Vasile Uleanu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.          

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1 Numărul \(\overline{3a5}\) este divizibil cu 9 pentru a =

(5p)     2. Daca \(\)\(a+\frac{1}{a}=3\)  ,  atunci \({{a}^{2}}+\frac{1}{{{a}^{2}}}=\)

(5p)     3. Numărul \(2\sqrt{8}+2\sqrt{18}\) scris sub forma \(\sqrt{n}\), unde n\(\in N\), este ……….

(5p)     4. Valoarea maximă a expresiei  E (x) = 27 – x² +4x   este  .....

(5p)     5 Aria unui hexagon regulat cu perimetrul de 24 cm este ……

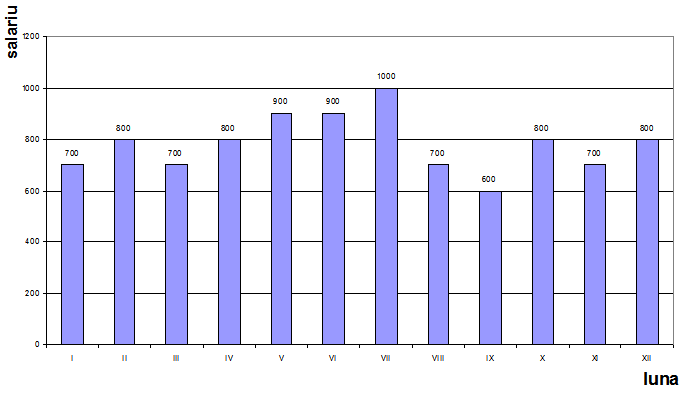
(5p)     6. Salariul pe ultimele 12 luni în lei  ale unui angajat se prezintă conform diagramei de mai jos.  Salariului obţinut pentru luna octombrie este …… lei

   SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o piramidă triunghiulară regulată VABC  cu vârful V .

(5p)     2. Simplificaţi : \(\frac{\left( {{x}^{2}}+2x+4 \right)\cdot \left( {{x}^{2}}+2x \right)+4}{\left( {{x}^{2}}+2x \right)\cdot \left( {{x}^{2}}+2x+3 \right)+2}\)

(5p)     3. Să se determine numerele reale x, y pentru care  :\(3{{x}^{2}}-2\sqrt{3}x+{{y}^{2}}+6y+10=0\)

4. Suma a trei numere este 101 . Dacă se micşorează primul număr cu 25% din el , al doilea se măreşte cu 75% din el , iar al treilea se dublează  , atunci numerele obţinute sunt egale .

(5p)    a) Să se afle numerele .

(5p)    b) Cât la sută este al treilea număr din al doilea număr?

(5p)     5. Arătaţi că fracţia \(\frac{2n+7}{5n+17}\)  este ireductibilă \(\forall \)n\(\in \)N.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. La o staţie PECO  depozitarea benzinei se face într-un recipient metalic care are  forma  de prismă patrulateră regulată ABCDA'B'C'D' . Recipientul are aria totală de 168  m² şi aria laterală de  96 m²  .

 (5p)  a) Aflaţi câţi  litri de benzină poate fi depozitaţi în recipient când este încărcat la capacitatea maximă.

 (5p)  b)Care este suma totală încasată din vânzarea benzinei aflată în recipient dacă 1litru de benzină este vândut cu 4,70 lei .

 (5p)  c) Unitatea PECO  plăteşte 80% din totalul încasărilor la rafinăria de unde a primit  benzina   şi restul  rămâne patronului pentru cheltuielile staţiei  . Ce sumă a  rămas patronului ?  

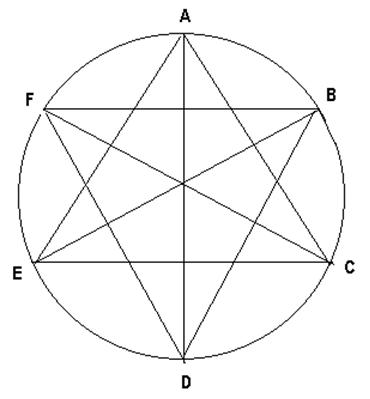
 2. În figura de mai jos vârfurile hexagonului regulat ABCDEF reprezintă ieşirile din oraş spre şoseaua de centură a unui oraş. Ştiind că diagonalele hexagonului sunt principalele artere de circulaţie rutieră ale oraşului şi că aria triunghiului ABE este de \(50\sqrt{3}\)km² , să se afle :

(5p)  a)Distanţa parcursă de un autobuz pe ruta A-E-C .

(5p)  b)Cu ce viteză trebuie să circule un automobil pentru a parcurge integral  lungimea şoselei de centură în timp de 1h şi 15 minute  . Se va lua (\(\pi \)= 3,14 ).

(5p)  c)Să se afle câte artere principale are oraşul în interior şi să se arate că suma distanţelor acestor artere este mai mică decât 120\(\sqrt{3}\) km .