Varianta 174

Prof: Uruc Doina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul împărțirii numărului 642 la 6 este egal cu...

(5p)     2. Cel mai mare număr natural divizibil cu 5, scris cu 3 cifre diferite, este....

(5p)     3. Aria unui romb cu diagonalele de 5 cm și 8 cm este egală cu... cm²

(5p)     4. În cubul ABCDA’B’C’D’ , unghiul dintr dreptele BC și AD’ are măsura de ... ^o

(5p)     5. Se consideră funcția \(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=x-4\). Valoarea funcției pentru x = 2 este egală cu...

(5p)     6. Elevii unei clase au obținut la matematică următoarele medii:

Media clasei este egală cu...

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați pe foaia de examen o prismă triunghiulară regulată ABCA’B’C’.

(5p)     2. Un biciclist parcurge un drum în 3 zile. Astfel, în prima zi el parcurge 30% din distanță, în a doua zi \(\frac{5}{9}\) din rest, iar în a treia zi ultimii 28 km. Ce lungime a avut drumul parcurs?

(5p)     3. Aflați cel mai mic număr natural nenul care împărțit pe rând la 27 și 24 dă de fiecare dată restul 5.

 4. Fie expresia: \(E\left( x \right)=\left( \frac{x+1}{x-1}+\frac{3}{{{x}^{2}}-1}-\frac{x+3}{x-1} \right)\cdot \frac{{{x}^{2}}-4x+3}{7}\), \(x\in \mathbb{R}\backslash \left\{ \pm 1 \right\}\)

(5p)    a) Aduceți expresia la forma cea mai simplă.

(5p)    b) Determinați numerele naturale n pentru care \(E\left( n \right)\in \mathbb{Z}\).

(5p)     5. Să se scrie sub formă de interval mulțimea soluțiilor inecuației \(3\left( x+4 \right)-9\le 5x+1\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

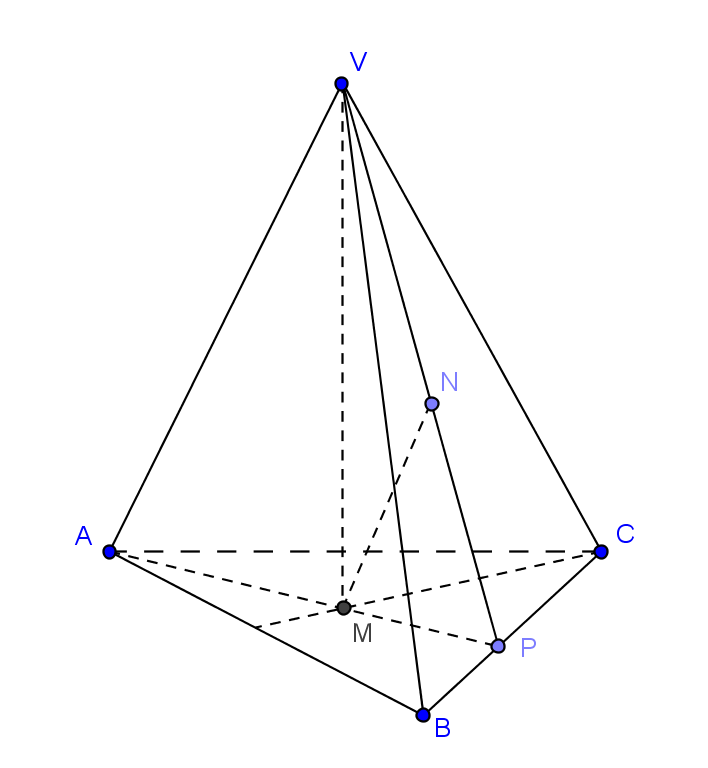
1. Mihai instalează în curte un cort sub forma unui tetraedru regulat VABC cu latura de 3m.

 (5p)  a) Calculați suprafața de pânză impermeabilă care a fost necesară confecționării cortului.

 (5p)  b) Cortul este întărit cu un suport MN, unde M și N sunt centrele de greutate ale fețelor ABC și VBC. Demonstrați că \(MN||\left( BAC \right)\) și calculați lungimea suportului.

 (5p)  c) Calculați aria și perimetrul triunghiului VAN.

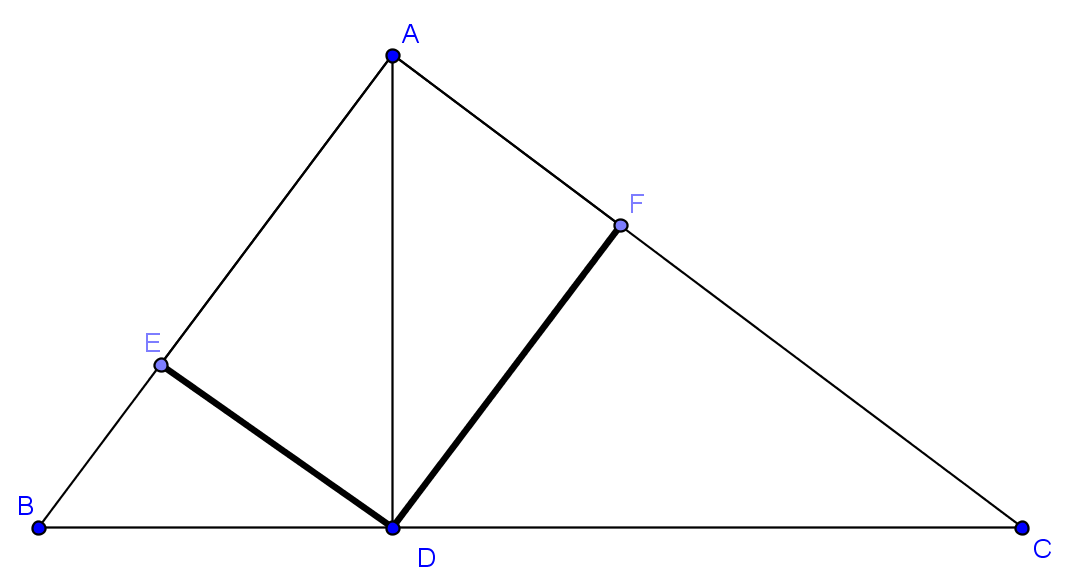
 2. O grădină are forma unui triunghi dreptunghic ABC , \(m\left( \sphericalangle A \right)={{90}^{o}}\), \(AD\bot BC\), \(AB=45m\), \(CD=48m\) și are două alei: \(\left[ DE \right]\bot \left[ AB \right]\), \(E\in \left( AB \right)\) și \(\left[ DF \right]\bot AC,F\in \left( AC \right)\).

(5p)  a) Între B și D se plantează gard viu. Calculați lungimea acestul gard.

(5p)  b) Pe suprafața BED se plantează ardei iar pe suprafața ACD roșii. Calculați raportul dintre suprafeța plantată cu ardei și cea plantată cu roșii.

(5p)  c) Calculați distanța dintre capetele E și F ale celor două alei.