Varianta 176

Prof: Boer Elena Milena

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului:\(25-5+3\)este egal cu ... .

(5p)     2. Dacă \(\frac{x}{3}=\frac{4}{6}\) atunci numărul\(2x+5\) este egal cu ... .

(5p)     3. Dacă \(A=[-3,5)\), atunci cardinalul mulțimii \(A\cap N\) este ... .

(5p)     4. Diagonala unui pătrat este \(2\sqrt{6}\)cm, atunci latura pătratului este egală cu ... cm.

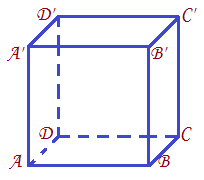
(5p)     5. În Figura 1 este reprezentat un cub ABCDA’B’C’D’. Măsura unghiului  determinat de dreptele AD’ și A’C’ este egală cu ... \(^{\circ }\).

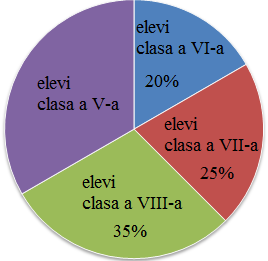
(5p)     6. În diagrama de mai jos, este reprezentată repartiția celor 200 de elevi ai unei școli participanți la o excursie, în raport cu clasa din care provin. Numărul elevilor de clasa a V-a este ... .

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenați pe foaia de examen, o piramidă triunghiulară regulată VABC.

(5p)     2. Arătați că numărul \(\left| \sqrt{7}-4 \right|+\frac{9}{4-\sqrt{7}}\) este număr natural.

(5p)     3. Un biciclist a parcurs un drum astfel: în prima zi un sfert din drum, a doua zi o  treime din rest, iar a treia zi două treimi din noul rest și încă 10 km. Aflați câți kilometri are drumul.

 4. Se consideră funcția \(f:R\to R,f(x)=-2x+3\).

(5p)    a) Reprezentați grafic funcția.

(5p)    b) Determinați punctul de pe graficul funcției care are coordonatele egale.

(5p)     5. Se consideră \(E(x)=-x{}^{2}-{{(x-2\sqrt{2})}^{2}}+2{{(\sqrt{2}-x)}^{2}}+4\). Arătați că \(\text{E}\left( \text{x} \right)\text{ }=\text{ }0\text{ }~\) pentru orice număr real x.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

   1. Figura 2 reprezintă schema unui loc de joacă. Se știe că ABCD este un pătrat și trapezul CFED are FC = CD = DE = 60 m iar unghiul CFE are măsura de \({{60}^{\circ }}\).

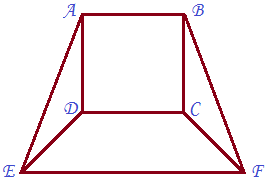
 (5p)  a) Aflați aria trapezului ABFE.

 (5p)  b) Arătați că aria triunghiului FBC este \(900\,{{m}^{2}}\).

 (5p)  c) Pentru fiecare metru pătrat al suprafețelor FBC și EDA sunt necesare 15 flori. Determinați ce sumă este necesară pentru plantarea florilor știind că o floare costă  1,5 lei și la peste 10000 de flori cumpărate se face o reducere de \(12%\).

 2. Figura 3 reprezintă schița unei bucăți de lemn având forma unui con circular drept. Distanța de la centrul bazei la generatoare este  cm. Unghiul dintre înălțimea și generatoarea conului este de .

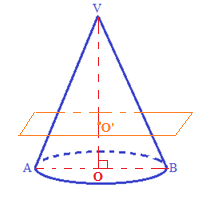
(5p)  a) Aflați aria totală a conului.

(5p)  b) Aflați volumul conului.

(5p)  c) Conul se secționează cu un plan paralel cu planul bazei la o distanță de din înălțimea acestuia. Determinați raportul dintre volumul conului și trunchiului de con obținute  prin secționare.