Varianta 191

Prof: Mocanu Ana-Gabriela

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului 728:7 este egal cu....

(5p)     2. Dacă b este un număr real nenul şi \(\frac{a}{32}=\frac{2}{b}\) atunci media geometrică a numerelor a şi b este egală cu....

(5p)     3.Intervalul [-3;2) conţine ...numere întregi.

(5p)     4. Pătratul ABCD are diagonala de 4 cm.Atunci aria pătratului ABCD este egală cu...\(\)\(c{{m}^{2}}\)

(5p)     5.Un trunchi de piramidă patrulateră regulată are latura bazei mari egală cu 5 cm,latura bazei mici egală cu 4cm şi înălţimea trunchiului egală cu 3cm.Atunci volumul trunchiului de piramidă este egal cu ...\(c{{m}^{3}}\).

 (5p)    6. Temperaturile înregistate în fiecare zi dintr-o săptămână , la ora 12:00 sunt prezentate în tabelul următor

    Diferenţa dintre cea mai mare temperatură şi cea mai mică temperatură este de ....\({}^\circ \)           

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o prismă hexagonală regulată ABCDEFA’B’C’D’E’F’.

(5p)     2. Calculaţi media aritmetică a numerelor \(a=\sqrt{{{\left( 3-2\sqrt{3} \right)}^{2}}}\) şi b=\(\sqrt{{{\left( 3+2\sqrt{3} \right)}^{2}}}\).

(5p)     3. Dacă într-o sală de clasă se aşază câte un elev într-o bancă,rămân 7 elevi în picioare,iar dacă se aşază câte 2 elevi într-o bancă,iar într-o bancă se aşază unul singur, rămân 5 bănci libere.Câte bănci sunt în sala de clasă?

 4. Se consideră funcţia f: \(\mathbb{R}\to \mathbb{R}\),\(f\left( x \right)=2x-2\).

(5p)    a)Aflaţi aria triunghiului AOB, unde \(A\) şi \(B\) sunt punctele de intersecţie  a graficului funcţiei \(f\)cu axele \(Ox\) ,respectiv \(Oy\) ale sistemului de coordonate \(xOy\).

(5p)    b)Aflaţi punctul situat pe reprezentarea geometrică a graficului funcţiei f care are coordonatele egale.

(5p)     5. Se consideră expresia \(E\left( x \right)=\left( \frac{2}{x+1}-\frac{2}{1-{{x}^{2}}}-\frac{1}{x-1} \right)\cdot \left( {{x}^{2}}-x-2 \right)\), unde \(x\) este număr real,\(x\ne -1\) şi \(x\ne 1\). Determinaţi numărul real m ,\(m\ne -1\) şi \(m\ne 1\),ştiind că \(E\left( m \right)=2\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Figura1. reprezintă un teren sub forma trapezului ABCD,parcelat în două parcele.Cunoaştem \(CM\parallel AD\),AB=40m,BC=1,2dam,CD=200dm şi AD=16m.

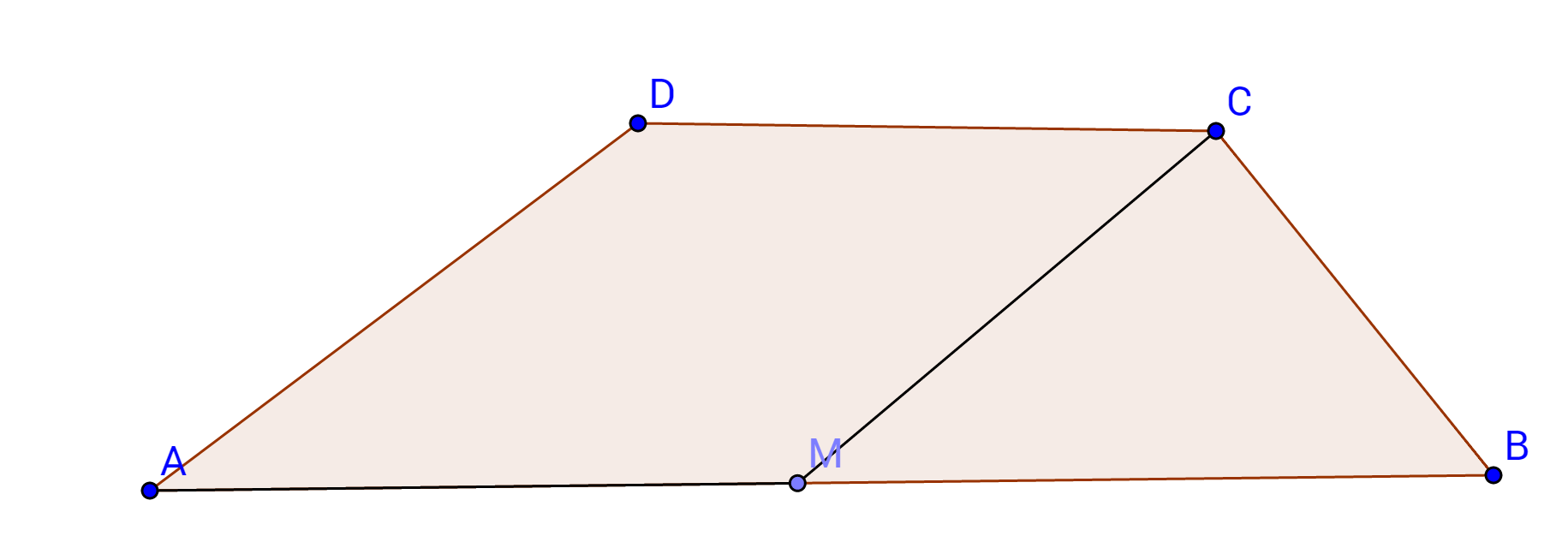
 (5p)  a)Aflaţi perimetrul terenului 

 (5p)  b)Arătaţi că suprafaţa parcelei MCB nu depăşeşte 1 ar.

 (5p)  c)Ce procent reprezintă suprafaţa parcelei ADCM dintr-un hectar?

2. Un con circular drept are raza bazei egală cu 15 cm şi generatoarea egală cu 25 cm.

(5p)  a)Aflaţi aria laterală a conului.

(5p)  b)Arătaţi că volumul conului este mai mic decât 5\(l\).Se consideră cunoscut faptul că \(3,14<\pi <3,15\).

(5p)  c)La ce distanţă de vârful conului trebuie dus un plan paralel cu baza astfel încât aria laterală  a trunchiului de con să fie de trei ori mai mare decât aria laterală a conului mic obţinut prin secţionare.