Știri Matematică 2018 - 2019
- Detalii
- Categorie: Știri Matematică 2018 - 2019
- Accesări: 164393
Calendarul Olimpiadei Naționale de Matematică 2017
Etapa pe școală – decembrie 2016
Etapa locală/pe sector al municipiului București – 21 ianuarie 2017
Etapa județeană – 18 martie 2017
Etapa națională – aprilie 2017, Timișoara
Calendarul olimpiadelor naționale și concursurilor județene 2017
Subiecte OLM gimnaziu și liceu 2015 - 2017
Etapa judeteana
Olimpiadă Matematică Gimnaziu || Subiecte, rezolvări 2016, 2015
Olimpiadă Matematică Liceu|| Subiecte, rezolvări 2016, 2015
Etapa locala
Olimpiada de Matematică Gimnaziu și Liceu - etapa locală 2017 din toate județele
Olimpiada de Matematică Gimnaziu și Liceu - etapa locală 2016 din toate județele
Olimpiada de Matematică Gimnaziu și Liceu - etapa locală 2015 din toate județele
- Detalii
- Categorie: Știri Matematică 2018 - 2019
- Accesări: 51349
PROBLEMA LUNII IANUARIE 2017

REVISTA ELECTRONICĂ MATEINFO.RO - IANUARIE 2017 (CLICK)
- Detalii
- Categorie: Știri Matematică 2018 - 2019
- Accesări: 75433
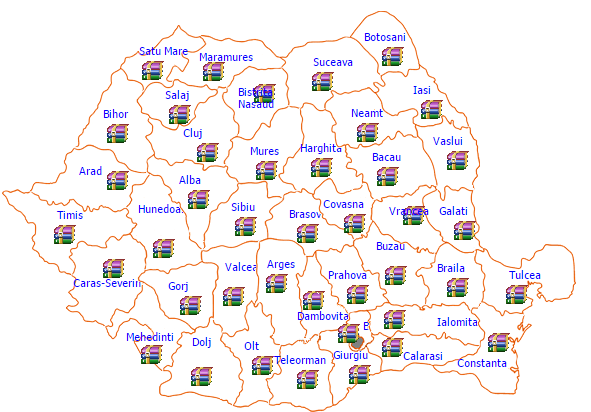
-
- Satu Mare
- Maramures
- Suceava
- Botosani
- Bihor
- Salaj
- Cluj
- Bistrita Nasaud
- Mures
- Harghita
- Neamt
- Iasi
- Arad
- Alba
- Sibiu
- Hunedoara
- Brasov
- Covasna
- Bacau
- Vaslui
- Galati
- Vrancea
- Timis
- Caras-Severin
- Gorj
- Valcea
- Arges
- Dambovita
- Prahova
- Buzau
- Braila
- Mehedinti
- Dolj
- Olt
- Teleorman
- Giurgiu
- B
- Ialomita
- Calarasi
- Constanta
- sursa: ssmr.ro
- Detalii
- Categorie: Știri Matematică 2018 - 2019
- Accesări: 58149
Problema lunii FEBRUARIE 2017
REVISTA ELECTRONICĂ MATEINFO.RO
8 ANI DE APARIȚII LUNARE
Să se arate că dacă punctele \(A,B,C,D,O,M\) din spaţiu îndeplinesc condiţiile: \(AB\bot CD,\,\,AD\bot BC,\,\,OA\bot BD\) şi \(M=p{{r}_{BD}}C\), atunci punctele \(A,C,O,M\) sunt coplanare.
Prof. C. Telteu, Constanţa
Așteptăm soluții cât mai interesante până pe data de 4.03.2017 pe adresa de e-mail a redacției (click).
Pagina 1 din 3