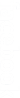MODEL 1 - EVALUARE NAȚIONALĂ MATEMATICĂ
- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.
- Timpul efectiv de lucru: 2 ore.
SUBIECTUL I – Pe foaia de examen se trec doar rezultatele. ( 30 de puncte)
(5p) 1. Rezultatul calculului \(\frac{1}{2}+0,5\)este egal cu….
(5p) 2. Dacă \(\frac{3}{4}=\frac{x}{2}\)atunci \(4\cdot x+4\)este egal cu….
(5p) 3. Cel mai mare număr întreg ce nu aparține intervalului \((2017;+\infty )\) este …
(5p) 4. Triunghiul isoscel \(ABC\) cu \(AB=AC\) are \(m\left( \widehat{A} \right)={{70}^{o}}.\) \(m\left( \widehat{B} \right)=\)….. grade.
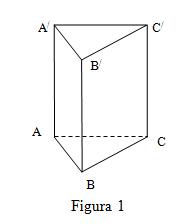
(5p) 5. În figura 1 este reprezentată prisma triunghiulară regulată \(ABC{{A}^{'}}{{B}^{'}}{{C}^{'}}\) cu latura bazei \(AB=6cm\) şi muchia laterală \(A{A}'=8cm\). Lungimea segmentului \(\left[ B{C}' \right]\) este egală cu…...\(cm\).
(5p) 6. Vârsta elevilor care participă la concursul de matematică „Pitagora” este reprezentată în tabelul de mai jos. Numărul elevilor cu vârsta peste 11 ani este .........
| Vârsta | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Nr. elevi | 1 | 4 | 6 | 3 | 6 | 4 | 1 |
SUBIECTUL II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)
(5p) 1. Desenaţi, pe foaia de examen, o prismă patrulateră regulată MATEINFO .
(5p) 2. Numerele naturale \(\overline{ab}\) și \(\overline{bc}\), scrise în baza zece, sunt direct proporționale cu numerele 5 și respectiv 3. Determinați toate numerele \(\overline{ab}\) și \(\overline{bc}\)care îndeplinesc condiția din enunț.
(5p) 3. Un călător a parcurs un drum în trei etape: în prima etapă a parcurs 20% din întregul drum şi încă 10 km.În a doua etapă a parcurs 50% din rest şi încă 17 km, iar în a treia etapă a parcurs ultimii 30 km.Ce lungime are întregul drum?
4. Fie functia f: R → R, f(x) = ax+b
(5p) a) Determinați funcția f(x) știind că f(1)+ f(3)= f(2) și f(-1)= - 6
(5p) b) Pentru a=2 și b= - 4 calculați distanța de la originea axelor la graficul funcției.
(5p) 5. Se dă expresia \[E\left( x \right)=\left( \frac{2x}{x+1}+\frac{2}{x-1}+\frac{4x}{{{x}^{2}}-1} \right)\cdot \left( \frac{2x}{x+1}+\frac{2}{x-1}-\frac{4x}{{{x}^{2}}-1} \right)\]cu \(x\in R-\left\{ -1;1 \right\}.~~\) Arătați că \(E\left( x \right)=4.\)
SUBIECTUL III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)
1. Figura 2 reprezintă modelul unei plăci de gresie în formă de pătrat \(ABCD\). Se ştie că \(AE=BF=20cm,\text{ }DE=CF=15cm\)şi \(m\left( \widehat{AED} \right)=m\left( \widehat{BFC} \right)={{90}^{o}}\), aflaţi:
(5p) a). Perimetrul pătratului \(ABCD\).
(5p) b). Arătaţi că lungimea segmentului \(\left[ EF \right]\)este \(1cm\).
(5p) c). Aflaţi aria trapezului isoscel \(ABFE\).
2. O pastilă (figura 3) are formă de cilindru circular drept ce are alipite la capete câte o semisferă ce are aceeaşi rază cu raza cilindrului, de 5 mm. Înălţimea cilindrului este de 15 mm.
(5p) a) Care este lungimea acestei pastile?
(5p) b) Care este volumul acestei pastile, în cm3;
(5p) c) Câte astfel de pastile încap într-o cutie care are formă de paralelipiped dreptunghic cu dimensiunile de L = 15 cm, l = 10 cm şi h = 2,5 cm.
(Figura 3)
BAREM MODEL 1 EVALUARE NAȚIONALĂ MATEMATICĂ