MODEL 2 - EVALUARE NAȚIONALĂ MATEMATICĂ

www.mateinfo.ro 

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(2-{{2}^{0}}\cdot {{0}^{2}}\)este ...

(5p)     2.  Dacă \(\frac{a}{b}=\frac{3}{4}\) și 2a+b=20, atunci media aritmetică a numerelor a și b este ...

(5p)     3. Cel mai mare număr întreg care nu aparține intervalului \((-2;+\infty )\) este …

(5p)     4. Un dreptunghi are lăţimea de 10 cm şi perimetrul de 100 cm. Atunci aria  dreptunghiului este  … cm².

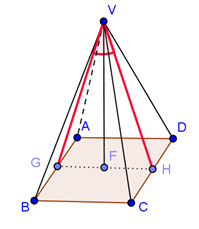
(5p)     5. În piramida patrulateră regulată VABCD notăm cu G mijlocul segmentului \(\left[ AB \right]\)şi

cu H mijlocul segmentului \(\left[ CD \right]\). Ştiind că VG=AB,  măsura unghiului \(\widehat{GVH}\) este de .....\(^{0}\).

(5p)     6. În urma unui test elevii unei clase au obţinut notele redate în tabelul de mai jos:

Media notelor din intervalui [6;8] screisă sub formă de fracție zecimală este  ....

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen un cilindru circular drept, cu raza unei baze şi axa de rotaţie.

(5p)     2. Arătați că numărul \(\overline{37a}+\overline{7a3}+\overline{a37}\) este divizibil cu 37, oricare ar fi cifra a nenulă.

(5p)     3.  Într-o expediție participă de două ori mai mulți geologi decât biologi. După o  săptămâna pleacă 20 geologi și sosesc 18 biologi. Astfel numărul geologilor și biologilor devine egal. Câți biologi au fost prezenți la începutul expediției?

           4. Se dă funcţia \(f:\mathbb{R}\to \mathbb{R},\,\,f\left( x \right)=-x+2,\,\,\forall x\in \mathbb{R}.\)

(5p)    a)  Reprezentaţi în plan punctele \(A={{G}_{f}}\cap Ox\)  şi  \(B={{G}_{f}}\cap Oy\) iar apoi graficul

                funcţiei.

(5p)    b) Dacă \(C\left( -2;0 \right)\) şi \(D\left( 0;-2 \right)\), arătaţi că ABCD este pătrat.

(5p)     5. Arătaţi că numărul \(a=E\left( \sqrt{2} \right)-\frac{1}{\sqrt{2}}\in \mathbb{Z}\), unde

              \(E\left( x \right)=\left[ \frac{1}{x}+1+\left( x+\frac{1}{x} \right):\frac{{{x}^{2}}+1}{x\left( x+1 \right)} \right]:\left( x+1 \right);\,\,\,\,x\in \mathbb{R}\backslash \left\{ -1;0 \right\}\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

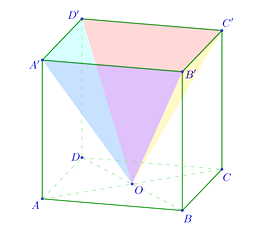
1. Un vas din metal (vezi figura alăturată) s-a obţinut din cubul \(ABCDA'B'C'D'\)  prin înlăturarea piramidei \(OA'B'C'D'\),  unde O este intersecţia diagonalelor ătratului ABCD.   Latura cubului este de 12 cm.

 (5p)  a) Încape un litru de apă în vas?

 (5p)  b) Dacă vasul este plin cu apă, care este aria suprafeţei unde?

 (5p)  c) Vasul este gol şi din interiorul său din punctul O pleacă o furnică. Mergând pe

              drumul cel mai scurt, furnica ajunge în punctul A.  Ce distanţă parcurge ea?

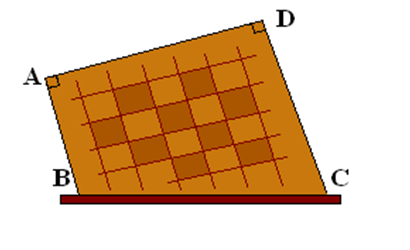
          2. În figura de mai jos este reprezentat un suport pentru şerveţele sub forma unui trapez dreptunghic ABCD cu AB || CD, \(m\left( \measuredangle \text{A} \right)=m\left( \measuredangle \text{D} \right)={{90}^{0}},\)AB = 7 cm, CD = 13cm , iar lungimile laturilor BC şi AD sunt direct proporţionale cu numerele 5 şi 4.

(5p)   a) Calculaţi lungimea laturii BC;           

(5p)   b) Calculaţi suprafaţa trapezului;

    (5p)   c) Calculaţi distanţa de la punctul D la baza BC a suportului.

Model 2 - Evaluare Națională la Matematică cls. a VIII a (SUBIECT ȘI BAREM) - APRILIE

https://www.facebook.com/www.mateinfo.ro/