Varianta 4

Prof: Andone Elena

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Dacă \(\left( 16+x \right)\cdot 2=14\), atunci x este egal cu …

(5p)     2. 3 muncitori termină o lucrare în 10 zile. 6 muncitori vor termina aceeaşi lucrare în……zile

(5p)     3. După o reducere cu 25% preţul unui produs este de 120 lei.Preţul iniţial al produsului a fost de … lei. 

(5p)     4. Intr-un trapez, baza mare are 6 cm şi baza mică este o treime din baza mare. Linia mijlocie a trapezului este agală cu … cm.

(5p)     5 Se consideră cubul ALGORITM. Măsura unghiului RLT este de……

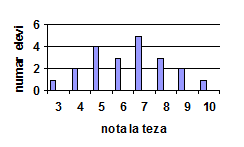
(5p)     6. Toţi elevii unei clase au susţinut teza la matematică. Rezultatele obţinute sunt reprezentate în graficul alăturat. Conform graficului, a obţinut cel puţin nota 8 un număr de  … elevi.

           SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o prismă hexagonală regulată ABCDEF A`B`C`D`E`F`.

(5p)     2. Fie mulţimea \(A=\left\{ -12;+3;2,94;\sqrt{2};\frac{1}{2};\frac{4}{2};-\sqrt{3};0;\pi  \right\}\). Aflaţi cardinalul mulţimii      \(A\cap Q\)

(5p)     3. Într-o clasă sunt 25 de elevi. 17 elevi cunosc foarte bine limba engleză  şi 18 elevi cunosc foarte bine limba franceză.Câţi elevi cunosc ambele limbi străine foarte bine?

            4. Fie funcţia liniară \(f:\mathbb{R}\to \mathbb{R}\) , f(x)=ax+b.

 (5p)     a)Determinaţi funcţia ştiind că graficul său trece prin punctele A(1,-4) şi B(-2,2).

(5p)      b) Pentru a=-2 şi b=-2 reprezentaţi grafic funcţia.

 (5p)     5. Să se arate că \(F(x)=\frac{{{x}^{2}}+6x+5}{{{x}^{2}}+2x-15}=\frac{x+1}{x-3}\) pentru orice \(x\in R\backslash \{-5;3\}\)

  SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

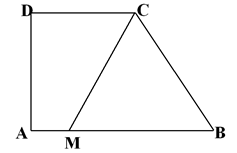
  1. În figura alăturată este ilustrată schematic schiţa unei

grădini  ABCD. AB =15 m, CD = 9 m, AD = 8 m. Grădina este împărţită printr-un strat de flori CM asfel încât aria suprafeţei MBC să fie egală cu aria suprafeţei CDAM.  Punctul M este situat pe AB astfel încât \(AM=x\); (x este o distanţă exprimată în metri; \(0<x<15)\).

(5p)  a) Să se exprime în funcţie de x, aria suprafeţei CDAM

 (5p)  b) Să se arate că aria suprafeţei MBC este egală cu  \(4\left( 15-x \right){{m}^{2}}\).

 (5p)  c) Dacă x = 3 m să se calculeze lungimea stratului cu flori .

          2. Un depozit de cereale are forma unui paralelipiped dreptunghic cu lungimea de 24 m, lăţimea 16m şi înălţimea 20 m.

 (5p)  a)Calculaţi aria laterală a depozitului

 (5p)  b)Se vopseşte suprafaţa laterală şi interior şi exterior.Dacă 1m² consumă 25 grame de vopsea aflaţi câte kilograme de vopsea sunt necesare.

 (5p)  c) Un kilogram de vopsea costă 40 lei.Dacă se cumpără mai mult de 50kg,se acordă o reducere de 20%  pentru întreaga cantitate de vopsea cumpărată. Cât a costat vopseaua?