Varianta 15

Prof: Badea Daniela

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului \(x\left( x+1 \right)-{{x}^{2}}\)este…..

(5p)     2. Într-o clasă cu 24 elevi, procentul de promovabilitate la un test a fost de 62,5%. Numărul elevilor care nu au promovat este egal cu ….

(5p)     3.Soluţia ecuaţiei \(3\sqrt{3}x-\sqrt{54}=0\)este…..

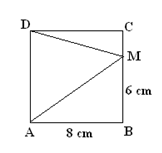
 (5p)     4.Pătratul ABCD din figura alăturată are latura de 8cm,\(\text{M}\in \left( \text{BC} \right)\)  şi AM= 6cm. Raportul dintre perimetrul trapezului AMCD şi perimetrul pătratului ABCD este egal cu …

(5p)     5. Volumul unei prisme triunghiulare regulate este \(6\sqrt{3}\text{ c}{{\text{m}}^{\text{3}}}\), iar muchia laterală este triplul laturii bazei. Aria laterală a prismei este …. cm².

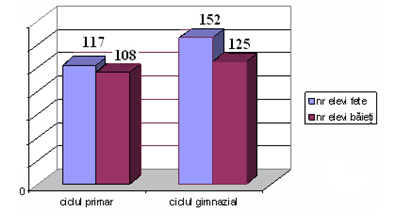
(5p)     6. În diagrama alăturată este reprezentat numărul de fete şi băieţi din cele două cicluri de învăţământ dintr-o şcoală generală. Numărul băieţilor este cu … mai mic decât cel al  fetelor.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, două plane perpendiculare,\(\alpha \)şi\(\beta \). 

(5p)     2. Media aritmetică a patru numere este 1904. Aflaţi numerele ştiind că primul număr reprezintă 60% din al doilea, al doilea reprezintă 60% din al treilea, iar al treilea reprezintă 60% din al patrulea.

(5p)     3. Fie numerele naturale a şi b cu proprietăţile următoare: \(\left( a+2b \right)\vdots 11\) şi \(a+6b=77\).

                             Arătaţi că \(b\vdots 11.\)

            4. Fie funcţia  \(f:\mathbb{R}\to \mathbb{R},\text{ }f\left( x \right)=x+1.\)

(5p)    a) Determinaţi funcţia\(g:\mathbb{R}\to \mathbb{R},\text{ g}\left( x \right)=mx+n\)ştiind că graficele celor două funcţii se intersectează în punctul M de abscisă 5, iar punctul \(\text{N}\left( \text{1;}-\text{2} \right)\in {{G}_{g}}\);

(5p)    b) Calculaţi aria poligonului determinat de graficele celor două funcţii cu axa ordonatelor.

(5p)    5. Determinaţi valoarea minimă a numărului

                                        \(\text{N=}\sqrt{{{x}^{2}}-4x+13}+\sqrt{{{y}^{2}}+6y+34}\text{ , unde }x,y\in \mathbb{R}.\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

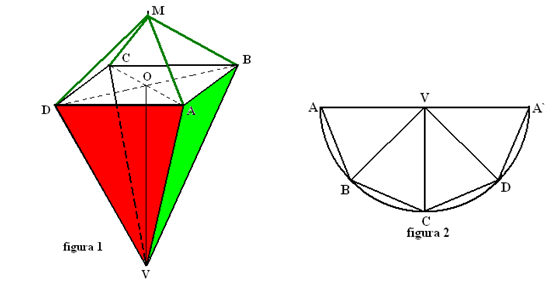
1. La o activitate practică, elevii unei clase confecţionează coşuleţe din carton, în formă de piramidă patrulateră regulată VABCD (vezi figura1). Ei decupează suprafaţa unui coşuleţ dintr-un semidisc de carton cu raza de 12 cm având pierdere minimă de material (vezi figura2).

(5p)  a) Câte coşuleţe vor decupa elevii, cu pierdere minimă de material, dintr-o coală de carton cu dimensiunile de 1,2m şi respectiv 0,85m?

(5p)   b) Arătaţi că \(\text{AB}\in \left( \text{9;10} \right);\)

(5p)  c) De capetele A şi C, respectiv B şi D se prind două bucăţi de pamblică de aceeaşi lungime astfel că în punctul M coşuleţul poate fi agăţat (punctele V,O şi M sunt coliniare), iar \(m\left( \measuredangle \text{MBO} \right)={{45}^{0}}\) . Cercetaţi dacă sunt suficienţi 12 m de pamblică pentru toate coşuleţele confecţionate din coala de carton.

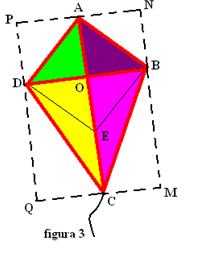
 2. Gabriel vrea să construiască un zmeu reprezentat schematic în figura 3, unde ABCE este pătrat de latură24 cm şi \(\Delta \text{BCD echilateral}\text{.}\) Pentru a fi rezistent el întăreşte zmeul cu baghetă de lemn de culoare roşie.

(5p)  a) Aflaţi lungimea totală a baghetei pe care o foloseşte  Gabriel;

(5p)    b) Calculaţi suprafaţa zmeului;

  (5p)    c) Calculaţi raportul dintre suprafaţa zmeului şi cea a dreptunghiului MNPQ din care este decupat.