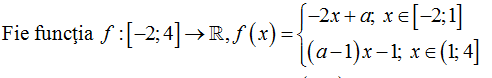Varianta 18

Prof: Badea Ion

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Dacă \(\frac{a}{3}=\frac{b}{5}\) atunci raportul \(\frac{5a+4b}{4a-b}\)are valoarea …

(5p)     2. Graficul funcţiei\(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=3x+m\) trece prin originea sistemului de axe de coordonate. Atunci m este egal cu ....

(5p)     3. Valoarea de adevăr a propoziţiei „ Perechea \(\left( 2;-3 \right)\)este soluţie a ecuaţiei \(3x-2y-12=0\)” este…

(5p)     4. Dimensiunile unui paralelipiped dreptunghic sunt direct proporţionale cu 12, 3 şi 4, iar diagonala sa are 26cm. Atunci suma lungimilor celor trei dimensiuni este…cm

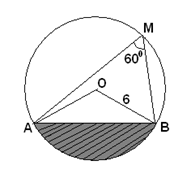
(5p)     5.În cercul de centru O şi rază R= 6 din figura alăturată, este înscris \(\Delta \text{MAB}\)cu\(m\left( \measuredangle \text{M} \right)={{60}^{0}}\) . Aria porţiunii haşurate este …

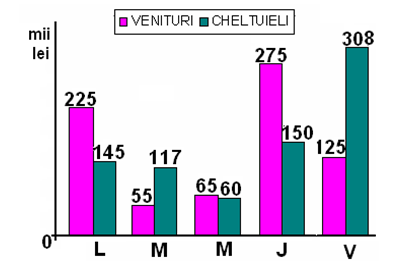
(5p)     6. Bugetul unei firme imobiliare (venituri şi cheltuieli) pe o săptămână este înregistrat în diagrama alăturată. Cheltuielile depăşesc veniturile cu ...... mii lei.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o prismă triunghiulară dreaptă PRISMA.

(5p)     2. Câte kg de fursecuri de 18 lei/kg trebuie amestecate cu 10 kg de fursecuri de 25 lei/kg pentru a putea vinde toată cantitatea cu 20 lei/kg şi suma încasată să fie aceeaşi în ambele cazuri?

(5p)     3. Arătaţi că \(N={{\left( \sqrt{3}-\sqrt{5} \right)}^{2}}+{{\left( \sqrt{3}+\sqrt{5} \right)}^{2}}-\sqrt{3}\left( \sqrt{5}-\sqrt{3} \right)+\sqrt{5}\left( \sqrt{5}+\sqrt{3} \right)\)este  număr natural.

            4. 

(5p)    a) Trasaţi graficul funcţiei ştiind că  \(A\left( 0;2 \right)\in {{G}_{f}}\);

(5p)    b) Pentru a =2 rezolvaţi ecuaţia \(f\left( x \right)=2\).

(5p)    5. Se consideră expresia \(E\left( x \right)={{x}^{4}}+2{{x}^{3}}+m{{x}^{2}}-12x+9\). Arătaţi că pentru orice \(m\ge 5\) \(E\left( x \right)\ge 0,\text{ }\left( \forall  \right)x\in \mathbb{R}.\)

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

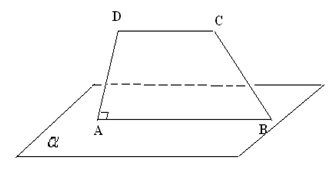
         1. Trapezul ABCD dreptunghic  în A are numai baza (AB) inclusă într-un plan \(\alpha \), iar proiecţiile punctelor C şi D pe planul \(\alpha \)sunt D` şi respectiv C`. Se ştie că \(\text{AB}=12\text{cm,}\) \(\text{CD=8cm, CC }\!\!\grave{\ }\!\!\text{ =4cm i }m\left( \measuredangle \left( \text{ABC} \right),\alpha  \right)={{30}^{0}}.\)

 (5p)  a) Demonstraţi că AB C`D` este trapez dreptunghic;

 (5p)  b) Calculaţi perimetrul trapezului AB C`D`;

 (5p)  c) Calculaţi aria totală a poliedrului AD D`BCC`;

           2. Un fermier deţine un teren agricol în formă dreptunghiulară care are lungimea cu 8 hm mai mare decât lăţimea, iar perimetrul lui este egal cu perimetrul unui alt teren în formă de pătrat cu suprafaţa de 484 ha. Fermierul împarte terenul său în trei parcele astfel încât raportul suprafeţelor primelor două este \(\frac{\text{3}}{\text{4}}\), iar al ultimelor două \(\frac{\text{4}}{\text{5}}\). Cea mai mică dintre parcele o cultivă cu legume: vinete, roşii şi cartofi, direct proporţional cu \(\frac{\text{4}}{\text{9}}\text{;}\frac{\text{1}}{\text{3}}\text{ si 0,}\left( \text{6} \right).\)Parcela cea mai mare o cultivă cu grâu, iar cea rămasă o transformă în  livadă de meri

(5p)  a) Calculaţi ariile celor trei parcele;

(5p)  b) Calculaţi ariile suprafeţelor cultivate cu legume;

(5p)  c) Producţia de grâu este de 5t/ hectar, iar kg de grâu costă 1,5lei. Din livadă s-au recoltat 40t/ hectar, care s-au vândut cu 2lei/kg. Ştiind că din vânzarea legumelor fermierul a obţinut o optime din suma încasată pe fructe, aflaţi suma totală încasată de fermier.