Varianta 20
Prof: Silvia Brabeceanu
- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.
- Timpul efectiv de lucru: 2 ore.
SUBIECTUL I – Pe foaia de examen se trec doar rezultatele. ( 30 de puncte)
(5p) 1. Rezultatul calculului \(72:8-2\cdot \left( -5 \right)\)este egal cu ……….
(5p) 2. Dacă \(A=\left\{ -5,-1,0,2,3 \right\}\)şi\(B=\left\{ -1,2,5,7,8 \right\}\)atunci mulţimea \(A\cap B\)este \(\left\{ ...,... \right\}\)
(5p) 3. Media aritmetică a numerelor \(a=\frac{3}{2}+\frac{1}{5}\)şi \(b=\frac{5}{2}-\frac{1}{5}\)este ……..
(5p) 4. Diametrul unui cerc este de \(10m\). Lungimea razei cercului este egală cu ……..\(cm\).
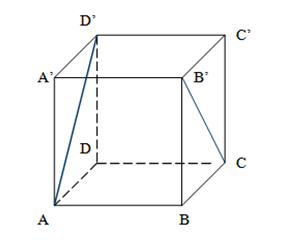
(5p) 5. Se consideră cubul \(ABCD{A}'{B}'{C}'{D}'\) din figura alăturată. Măsura unghiului dintre dreptele \(A{D}'\) şi \({B}'C\) este egală cu ………..
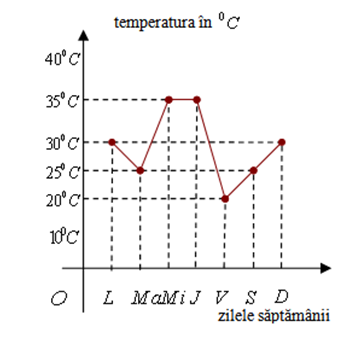
(5p) 6. Figura de mai jos reprezintă graficul evoluţiei temperaturilor maxime într-o săptămână de vară. Temperatura a scăzut de miercuri până vineri cu ……\(^{0}C\)
SUBIECTUL II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)
(5p) 1. Desenaţi, pe foaia de examen, o piramidă patrulateră regulată de bază MNPQ şi vârf S.
(5p) 2. Într-o librărie, pe un raft sunt 27 de cărţi, pe un alt raft se află de trei ori mai multe cărţi, iar pe al treilea raft \(\frac{2}{3}\)din numărul cărţilor aflate pe primele două rafturi. Câte cărţi sunt în total pe cele trei rafturi?
(5p) 3. Suma a cinci numere naturale consecutive este 50. Calculaţi produsul ultimelor trei numere.
4. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R},\text{ }f\left( x \right)=-5x+3\).
(5p) a) Reprezentaţi graficul funcţiei \(f\);
(5p) b) Determinaţi numărul real \(m\)pentru care punctul \(P\left( m+2,m-1 \right)\)este situat pe graficul funcţiei \(f\);
(5p) 5. Arătaţi că numărul \(a={{\left( \sqrt{7}+\sqrt{5} \right)}^{2}}-\sqrt{5}\left( \sqrt{7}+\sqrt{5} \right)-\sqrt{7}\left( \sqrt{5}-2\sqrt{7} \right)\)este natural.
SUBIECTUL III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)
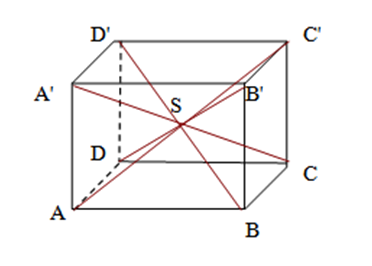
1. Figura 1. reprezintă un cub \(ABCD{A}'{B}'{C}'{D}'\)cu muchia de \(6dm\), iar \(S\)este punctul de intersecţie al diagonalelor cubului.
(5p) a) Aflaţi suma lungimilor muchiilor laterale ale piramidei \(SAD{D}'{A}'\);
(5p) b) Calculaţi aria laterală a piramidei \(SAD{D}'{A}'\);
(5p) c) Determinaţi măsura unghiului dintre planele \(\left( {A}'{B}'C \right)\) şi \(\left( AB{D}' \right)\);
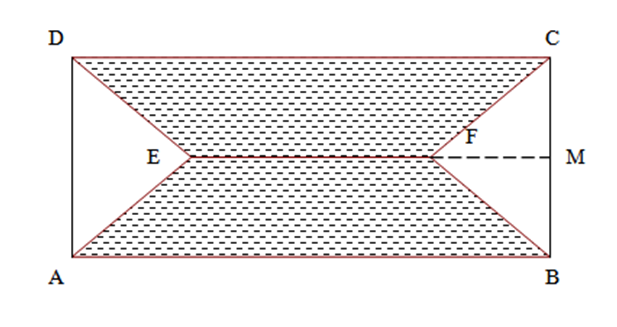
2. Figura alăturată reprezintă schiţa unei grădini dreptunghiulare în care porţiunea haşurată este formată din două trapeze isoscele având \(AB\parallel EF\parallel DC\), \(AE=DE=EF=6m\), \(AB=12m\).
(5p) a) Aflaţi lungimea segmentului \(\left[ FM \right]\)unde \(\left\{ M \right\}=EF\cap BC\);
(5p) b) Calculaţi aria porţiunii haşurate;
(5p) c) Determinaţi raportul dintre aria porţiunii nehaşurate şi cea a dreptunghiului \(ABCD\);