Varianta 21

Prof: Silvia Brabeceanu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(\left( \frac{3}{7}+\frac{5}{7} \right)\cdot \frac{14}{8}\)este egal cu ……..

(5p)     2. Numărul necunoscut din proporţia \(\frac{x}{4}=\frac{17}{51}\)are valoarea ……..

(5p)     3. Într-o urnă sunt 9 bile albe şi 11 bile roşii. Probabilitatea ca bila extrasă să fie roşie este egală cu …….. 

(5p)     4. Un pătrat \(ABCD\)cu latura de \(5cm\), are diagonala \(AC\)egală cu ……..\(cm\).

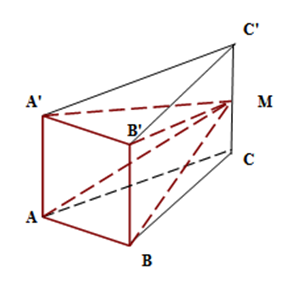
(5p)     5. Se consideră cubul \(ABCD{A}'{B}'{C}'{D}'\)din figura alăturată. Intersecţia planelor \(\left( AB{D}' \right)\)şi \(\left( {B}'{C}'C \right)\)este dreapta ……..

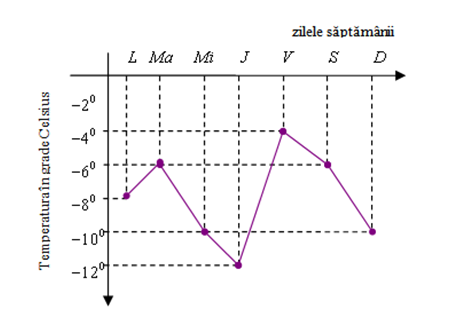
 (5p)     6. Figura de mai jos reprezintă graficul evoluţiei temperaturilor minime într-o săptămână de iarnă. În această săptămână temperatura maximă a fost de ……..\(^{0}C\).

     SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o piramidă triunghiulară regulată de bază MNP şi vârf V.

(5p)     2. O echipă de muncitori, într-o zi, au îmbuteliat 1250 sticle cu apă minerală, a doua zi au îmbuteliat cu \(\frac{2}{5}\)mai puţin decât în prima zi, iar în a treia zi cu \(\frac{3}{10}\)mai mult decât în a doua zi. Câte sticle au fost îmbuteliate în cele trei zile? 

(5p)     3. Raportul dintre suma şi diferenţa a două numere este \(\frac{5}{6}\). Să se afle numerele ştiind că \(20\)% din primul număr este cu 4 mai mare decât \(30\)% din al doilea număr. 

           4. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R},\text{ }f\left( x \right)=3x-1\).

 (5p)    a) Verificaţi dacă punctele \(A\left( 0,2 \right)\) şi \(B\left( -1,-4 \right)\)aparţin graficului funcţiei \(f\); 

(5p)    b) Pentru \(f\left( x \right)=3x-1\), determinaţi \(m\in \mathbb{R}\), astfel încât \(f\left( m+2 \right)+f\left( m-3 \right)=9\);

 (5p)     5. Să se aducă la forma cea mai simplă expresia

       \(E\left( x \right)=\left( \frac{1}{3x-4}-\frac{1}{3x+4} \right)\cdot \frac{9{{x}^{2}}+24x+16}{4}+\frac{4-3x}{3x-4},\text{ }x\in \mathbb{R}\backslash \left\{ \pm \frac{4}{3} \right\}\)

 SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

  1. Figura 1. reprezintă o piesă metalică în formă de prismă triunghiulară regulată, din care se obţine piramida \(MAB{B}'{A}'\), unde \(M\)este mijlocul muchiei \(\left( C{C}' \right)\). Se ştie că \(AB=A{A}'=10cm\). 

 (5p)  a) Aflaţi înălţimea piramidei; 

 (5p)  b) Calculaţi aria laterală a piramidei;             

  (5p)  c) Determinaţi volumul de metal ce se pierde;

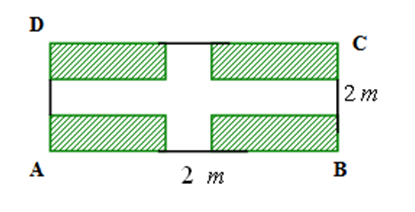
      2. Figura 2. reprezintă o suprafaţă de teren dreptunghiulară pe care sunt amenajate două alei, fiecare cu lăţimea de \(2m\), reprezentate în figură de porţiunea nehaşurată. Se ştie că \(AB=14m\) şi \(BC=8m\).

 (5p)  a) Aflaţi aria porţiunii haşurate; 

(5p)  b) Calculaţi suprafaţa ocupată de cele două alei; 

(5p)  c) Determinaţi volumul de pietriş necesar pentru pietruirea aleilor cu un strat gros de \(5cm\);