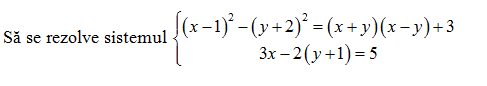Varianta 22

Prof: Silvia Brabeceanu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Dacă \(23-8+5-2x=30\)atunci numărul \(x\)este egal cu ……..

(5p)     2. Dacă \(a=6\)şi \(b+c=18\)atunci \(ab+ac\)este egal cu ……..

(5p)     3. Probabilitatea ca la aruncarea unui zar să apară un număr prim este …….. 

(5p)     4. Trapezul dreptunghic \(ABCD\) în care \(m\left( {\hat{A}} \right)=m\left( {\hat{D}} \right)={{90}^{0}}\), \(AB=15cm\), \(DC=7\), \(BC=10\), are perimetrul egal cu ……..

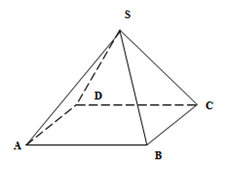
(5p)     5. Se consideră piramida regulată \(SABCD\), cu toate muchiile congruente. Măsura unghiului dintre dreptele \(SA\)şi \(DC\)este egală cu ……..

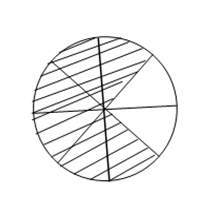
(5p)     6. În figura de mai jos discul a fost împărţit în 8 părţi egale. Porţiunea nehaşurată reprezintă din toată suprafaţa ……..%.

  SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un trunchi de  piramidă patrulateră regulată de baze  ABCD şi MNPQ.

(5p)     2. Se consideră mulţimea \(A=\left\{ x\in \mathbb{R}\left| -1\le 2x+3\le 7 \right. \right\}\). Enumeraţi elementele mulţimii \(A\cap \mathbb{N}\). 

(5p)     3. 

            4. Fie funcţiile \(f,g:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=x-1\) şi \(g\left( x \right)=2x-5\). 

(5p)    a) Determinaţi coordonatele punctului de intersecţie a graficelor celor două funcţii; 

(5p)    b) Să se rezolve ecuaţia: \(\left( f\left( x \right)+2 \right)\cdot g\left( x \right)=2{{\left( x-1 \right)}^{2}}+6x+3\); 

(5p)     5. Descompuneţi în produs expresia: \(E\left( x \right)={{\left( 3{{x}^{2}}+2 \right)}^{2}}-25{{x}^{2}}\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

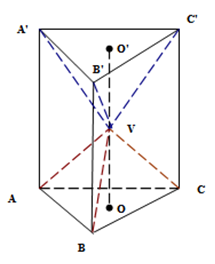
  1. Figura 1. reprezintă o piesă metalică în formă de prismă triunghiulară regulată din care se obţin piramidele \(VABC\)şi \(V{A}'{B}'{C}'\), având vârful \(V\)comun în mijlocul segmentului \(\left[ O{O}' \right]\); \(O\)şi \({O}'\) sunt ortocentrele celor două baze. Se ştie că \(AB=A{A}'=12cm\). 

 (5p)  a) Aflaţi volumul piramidei \(VABC\); 

 (5p)  b) Calculaţi volumul de material ce se pierde; 

 (5p)  c) Determinaţi volumul piramidei \(VAB{B}'{A}'\);

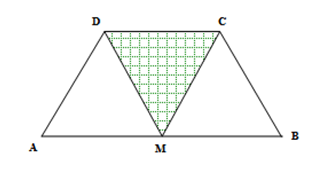
          2. Figura alăturată reprezintă o suprafaţă de teren în formă de trapez isoscel în care porţiunea haşurată este semănată cu gazon. Se ştie că \(AB=12m\), \(AD=DC=CB=6m\), iar \(M\) este mijlocul lui \(\left( AB \right)\).

 (5p)  a) Aflaţi aria trapezului; 

(5p)  b) Determinaţi raportul dintre aria suprafeţei cu gazon şi aria trapezului; 

(5p)  c) Demonstraţi că \(AD\)şi \(BD\)sunt perpendiculare;