Varianta 23

Prof: Silvia Brabeceanu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului $\left( \frac{5}{3}+\frac{9}{3} \right)\cdot \frac{9}{7}$este egal cu ……..

(5p)     2. Fie mulţimile $A=\left\{ x\in \mathbb{N}|x+1\le 5 \right\}$şi $B=\left\{ -3,-2,0,4 \right\}$. Mulţimea $A\cap B=\left\{ ...,... \right\}$

(5p)     3. Dintre numerele $x=\sqrt{2}$şi $y=1,45$mai mare este numărul…….. 

(5p)     4. Un cerc cu lungimea de $12\pi cm$are aria egală cu ……..

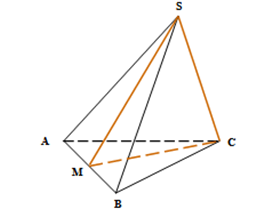
(5p)     5. Se consideră tetraedrul regulat $SABC$şi $M$mijlocul lui $\left[ AB \right]$. Laturile congruente ale triunghiului isoscel $SMC$sunt ……..

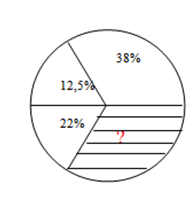
(5p)     6. În figura de mai jos este reprezentată printr-o diagramă circulară, repartizarea terenului unei ferme agricole. Porţiunea haşurată reprezintă ……..%.

  SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un trunchi de piramidă triunghiulară regulată de baze ABC şi A'B'C'. 

(5p)     2. Rezolvaţi în $\mathbb{R}$ecuaţia : $\frac{x-1}{2}+\frac{x}{5}=1-\frac{2x+3}{10}$. 

(5p)     3. Suma a trei numere naturale este $180$. Se ştie că suma dintre primul şi al treilea număr este de 3 ori mai mare decât al doilea şi că printre cele 3 numere se află şi cel mai mic număr prim de două cifre. Să se afle numerele. 

           4. Fie funcţia $f:\mathbb{R}\to \mathbb{R},\text{  }f\left( x \right)=-2x-3$ 

(5p)    a) Să se traseze graficul funcţiei $f$; 

(5p)    b) Să se determine $n\in \mathbb{Z}$ astfel încât $f\left( -2 \right)+f\left( -1 \right)+f\left( 1 \right)+f\left( 2 \right)+f\left( n \right)=15$; 

(5p)     5. Arătaţi că numărul $p={{\left( \sqrt{3}+\sqrt{2} \right)}^{2}}+2\left( \sqrt{3}+\sqrt{2} \right)\cdot \left( \sqrt{5}-\sqrt{2} \right)+{{\left( \sqrt{5}-\sqrt{2} \right)}^{2}}$nu este natural.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

  1. Figura de mai jos reprezintă un trunchi de con circular drept cu raza bazei mici $r=3cm$,  înălţimea $h=8cm$ şi volumul de$312\pi c{{m}^{3}}$.

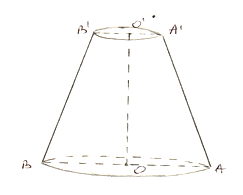
(5p)  a) Aflaţi aria secţiunii axiale a trunchiului de con.

(5p)  b) Aria laterală a conului din care provine trunchiul de con.

(5p)  c) Sinusul unghiului dintre două generatoare diametral opuse ale trunchiului de con.

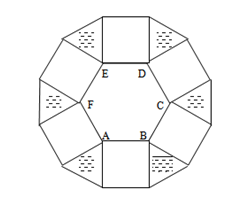
 2. Figura de mai jos reprezintă o suprafaţă în care $ABCDEF$este un hexagon regulat cu latura de $6m$, iar pe laturile acestuia s-au construit în afară pătrate. 

(5p)  a) Aflaţi aria porţiunii nehaşurate din exteriorul hexagonului; 

(5p)  b) Determinaţi perimetrul întregii suprafeţe; 

(5p)  c) Comparaţi aria porţiunii haşurate cu aria hexagonului $ABCDEF$;