Varianta 25

Prof: Ionel Brabeceanu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(0,5+3,2:2\) este ……..

(5p)     2. \(15%\)din 1200 este ……..

(5p)     3. Dacă \(\frac{5x}{6y}=\frac{10}{4}\), atunci \(\frac{x}{y}\) este egal cu …….. 

(5p)     4. Într-o livadă în formă de dreptunghi cu \(L=15m\) şi \(l=8m\), se plantează pomi fructiferi. Pentru a fi plantaţi toţi pomii, lungimea se măreşte cu \(\frac{3}{4}\)din lăţime. Lungimea dreptunghiului este de ……..\(m\).

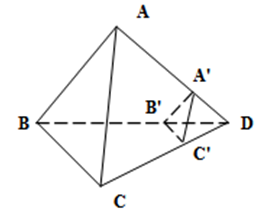
(5p)     5. În figura alăturată, \(ABCD\)este un tetraedru regulat, iar planele \(\left( {A}'{B}'{C}' \right)\)şi \(\left( ABC \right)\)sunt paralele. Măsura unghiului dintre dreptele \({A}'{C}'\)şi \(AB\)este egală cu ……..\(^{0}\).

(5p)     6. În tabelul de mai jos fiecărui număr din prima linie îi corespunde un număr din a doua linie. Numărul ce corespunde lui \(-1\)este ……..

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi o piramidă regulată cu baza hexagonul\(ABCDEF\) şi vârf \(M\). 

(5p)     2. O echipă de muncitori trebuia să altoiască câte 50 de butuci de vie zilnic. Muncitorii au altoit în fiecare zi câte 56 de butuci şi a terminat lucrarea cu 3 zile mai devreme, depăşind planul cu 120 de butuci altoiţi. Să se afle în câte zile echipa a terminat lucrarea. 

(5p)     3. Să se simplifice expresia:  \(E\left( x \right)=\frac{\left( {{x}^{2}}-9 \right)\left( {{x}^{2}}-25 \right)}{\left( {{x}^{2}}+10x+25 \right)\left( {{x}^{2}}+6x+9 \right)}\) 

           4. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R}\), \(f\left( x \right)=ax+5\), \(a\in {{\mathbb{R}}^{*}}\).

 (5p)    a) Să se determine \(a\)ştiind că \(A\left( -2,1 \right)\)este situat pe graficul funcţiei \(f\); 

(5p)    b) Pentru \(a=2\)să se reprezinte graficul funcţiei \(f\); 

(5p)     5. Să se rezolve inecuaţia:  \(12-3\left( x+4 \right)\le -5x+6\).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

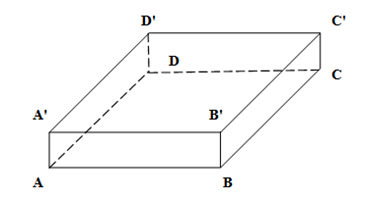
  1. În figura alăturată, este reprezentată o cutie în formă de paralelipiped dreptunghic \(ABCD{A}'{B}'{C}'{D}'\) cu \(A{A}'=12cm\). În cutie se află apă până la înălţimea de \(2cm\). Dacă aşezăm cutia având baza \(BC{C}'{B}'\), apa se ridică la înălţimea de \(3cm\), iar dacă o aşezăm având baza \(AB{B}'{A}'\)apa se ridică la înălţimea de \(4cm\).

 (5p)  a) Să se afle dimensiunile cutiei; 

 (5p)  b) Câtă apă conţine cutia;                               

 (5p)  c) Stabiliţi dacă în cutie încap \(5,2l\)de apă.

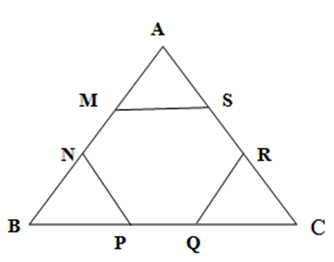
  2. Un elev şi-a propus să obţină dintr-o bucată de hârtie de formă triunghi echilateral, un hexagon regulat tăind vârfurile triunghiului aşa ca în figură. Se ştie că \(AB=12cm\).

(5p)  a) Demonstraţi că \(AM=MN\); 

(5p)  b) Aflaţi lungimea laturii hexagonului; 

(5p)  c) Arătaţi că aria hexagonului este \(\frac{2}{3}\)din aria triunghiului;