Varianta 27

Prof: Ionel Brabeceanu

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului $6-6\cdot 5+{{5}^{2}}$este numărul ……..

(5p)     2. Produsul inverselor numerelor  $-3$şi $\frac{1}{2}$este numărul ……..

(5p)     3. Media geometrică a numerelor $a=2+{{4}^{2}}-9$şi $b=\frac{11}{4}+\frac{13}{4}-2$este numărul …….. 

(5p)     4. Un triunghi dreptunghic isoscel are catetele egale cu $10cm$. Aria triunghiului este …….. $c{{m}^{2}}$.

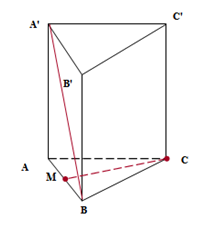
(5p)     5. $ABC{A}'{B}'{C}'$este o prismă regulată dreaptă, iar $M$este mijlocul muchiei $\left[ AB \right]$. Măsura unghiului dintre dreptele ${A}'B$şi $CM$este egală cu ……..

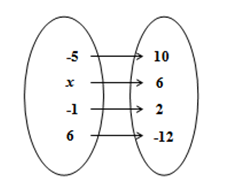
(5p)     6. În figura de mai jos fiecare element al mulţimii $B$corespunde unui element din mulţimea $A$. Numărul 6 corespunde numărului ……..

           SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Construiţi o prismă patrulateră regulată $ABCDMNPQ$. 

(5p)     2. Dacă scădem 8 dintr-un număr necunoscut şi înmulţim diferenţa cu 12, iar la produsul obţinut adăugăm dublul numărului necunoscut, obţinem 44. Să se afle numărul necunoscut. 

(5p)     3. O secţie de croitorie trebuie să confecţioneze $800$de costume bărbăteşti. Într-o primă etapă, s-au confecţionat 128 de costume. Câte procente din numărul de costume reprezintă cele confecţionate. 

           4. Se consideră funcţia $f:\mathbb{R}\to \mathbb{R},\text{  }f\left( x \right)=mx+1,\text{  }m\in \mathbb{R}$. 

(5p)    a) Să se determine $m\in \mathbb{R}$astfel încât punctul $A\left( 2,3 \right)$să se afle pe graficul funcţiei; 

(5p)    b) Pentru $m=1$să se calculeze $f\left( 0 \right)+f\left( 1 \right)+f\left( 2 \right)+\cdots +f\left( 69 \right)$; 

(5p)     5. Să se rezolve ecuaţia : $\left| x-1 \right|-\left| 2x-2 \right|+\left| 5x-5 \right|=4$.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

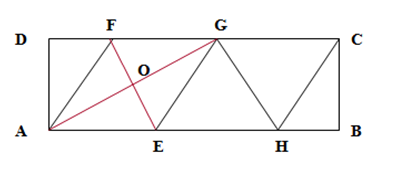
1. Figura alăturată reprezintă o suprafaţă dreptunghiulară $ABCD$, iar triunghiurile $AEF,\text{ }EFG,\text{ }EHG$şi $CHG$sunt echilaterale. Se ştie că $AB=20cm$. 

 (5p)  a) Aflaţi lungimea segmentului $\left[ FE \right]$; 

 (5p)  b) Calculaţi distanţa dintre  $A$şi $C$; 

 (5p)  c) Aflaţi aria triunghiului $AOD$unde $\left\{ O \right\}=AG\cap EF$;

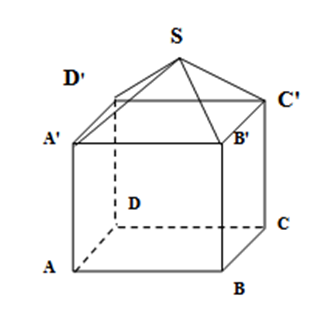
2. Un cort are forma unei prisme patrulatere regulată, iar deasupra o piramidă regulată. Latura bazei este de $4m$, înălţimea prismei de $2m$ şi înălţimea piramidei de $4,5m$. Pânza folosită pentru acest cort are lăţimea de $1,3m$. 

(5p)  a) Aflaţi volumul cortului; 

(5p)  b) Aflaţi suprafaţa cortului; 

(5p)  c) Câţi metrii de pânză se vor folosii;