Varianta 31

Prof: Breazu Nicolae.

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Rezultatul calculului \(47-27:3+2\) este....

(5p)     2. Dacă din vârsta tatălui scădem 5 ani, obţinem de trei ori vârsta fiului.Ştiind că suma celor două vârste este de 45 de ani, atunci vârsta fiului este...... ani.

(5p)     3. După majorarea cu un sfert, salariul unui muncitor este de 2000 lei. Salariul său înainte de această creştere era de ....... lei. 

(5p)     4. Un dreptunghi cu lungimea de  4cm este înscris într-un cerc cu raza de 2,5cm. Lăţimea dreptunghiului este de.....cm.

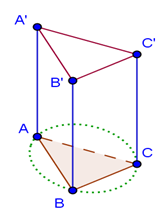
(5p)     5. Volumul prismei triunghiulare regulate ABCA’B’C’ din figură este de \(243{{m}^{3}}\).

Dacă raza cercului în care se poate înscrie baza este de \(3\sqrt{3}\,m\), atunci muchia AA’  are.....m.

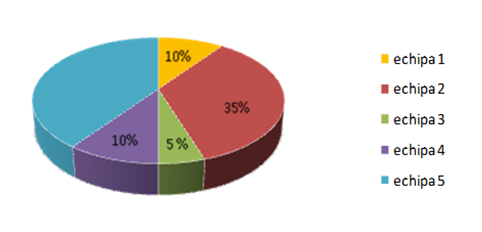
(5p)    6. La colectarea maculaturii, un colectiv de 30 de elevi a fost împărţit în 5 grupe. De-

senul alăturat arată contribuţia procentuală a fiecărei echipe la această acţiune. Ştiind că în total s-au strâns 500 kg de maculatură, echipa cea mai harnică a adunat.....kg.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi pe foaia de examen două drepte paralele tăiate de o secantă şi marcaţi două unghiuri alterne interne. 

(5p)     2. Se cunosc mulţimile \(A=\left\{ a\in \mathbb{N}\left| a\le 28\,\,si\,\,5\left| a \right. \right. \right\}\)şi \(A=\left\{ a\in \mathbb{N}\left| b<63\,\,si\,\,7\left| b \right. \right. \right\}\). Câte elemente au mulţimile \(A\cup B\) şi \(A\cap B\)? 

(5p)     3. Suma a două numere rele pozitive a şi b este 64. Dacă împărţim pe a la b obţinem câtul 3 şi restul 8. Determinaţi a şi b. 

            4. Fie expresia \(F\left( x \right)=\left( \frac{1}{x-1}-\frac{x+{{x}^{2}}}{{{x}^{3}}-2x+1} \right):\frac{x+1}{x-1}\), unde \(x\in \mathbb{R}\backslash \left\{ -1,1 \right\}\) 

(5p)    a) Să se arate că \({{x}^{3}}-2x+1=\left( x-1 \right)\left( {{x}^{2}}+x-1 \right)\). 

(5p)    b) Să se determine \(a\in \mathbb{R}\backslash \left\{ 1,-1 \right\}\)astfel încât \(F\left( a \right)=\frac{1}{1-{{a}^{3}}}\). 

(5p)     5. Demonstraţi că numărul \(\frac{\sqrt{2+\sqrt{3}}}{\sqrt{2-\sqrt{3}}}+\frac{\sqrt{2+\sqrt{2}}}{\sqrt{2-\sqrt{2}}}-\sqrt{5+2\sqrt{6}}\) este raţional.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.(30 de puncte)

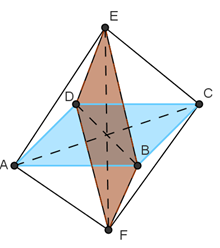
       1. Un diamant artificial este realizat prin lipirea bazelor a două piramide patrulatere regulate, ca în figură. Toate muchiile acestui corp au 1 cm. 

 (5p)  a) Calculaţi volumul corpului; 

 (5p)  b) Care este distanţa cea mai mare între două vârfuri ale diamantului? 

 (5p)  c) Secţiunea diagonală a diamantului este un patrulater congruent cu baza piramidei? Calculaţi aria bazei şi aria unei secţiuni diagonale.

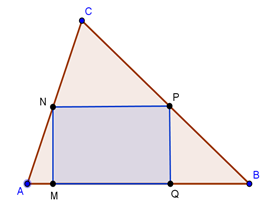
          2. Din materialul textil în forma unui triunghi ABC se decupează un dreptunghi MNPQ. Se ştie că AB=BC=13 şi AC=10. 

(5p)  a) Care este aria triunghiului ABC? 

(5p)  b) Care este aria dreptunghiului MNPQ dacă NP este linie mijlocie? 

(5p)  c) Punctele N şi P pot ocupa alte poziţii pe laturile [AC] respectiv [BC] astfel încât aria dreptunghiului MNPQ să fie mai mare decât rezultatul de la b)?