Varianta 33

Prof: Bulgăr Delia Valentina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

          

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

 

(5p)     1. Dacă 15-4+x-2=11,atunci numărul x este egal cu……………..

(5p)     2. De pe un teren cultivat cu roşii un ţăran obţine o recoltă de 4t roşii. Dacă ar dubla

                suprafaţa terenului cultivat cu roşii ţăranul ar obţine o recoltă de……..t roşii.

(5p)     3. Dacă un atlas costă 120 lei, după o scumpire cu 20% preţul atlasului va fi de …lei.

(5p)     4. Un triunghi are perimetrul egal cu 12cm. Atunci suma lungimilor liniilor mijlocii

                ale triunghiului este egală cu…… cm

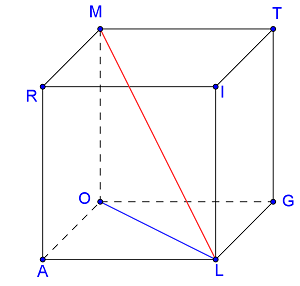
(5p)     5. Se consideră cubul ALGORITM din figura1. Dacă latura cubului este de 5cm,

                atunci tangenta unghiului dintre dreptele LM şi LO are valoarea de ……….

figura 1.

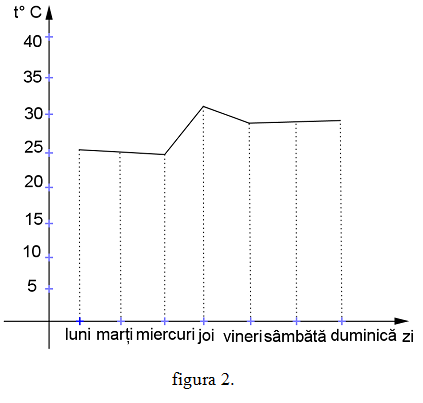
(5p)     6. În graficul din figura 2. sunt reprezentate temperaturile de la ora 12 dintr-o 

                săptămână a lunii iunie. Cel mai cald a fost în ziua de ……….

 

 

figura 2.

 

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

 

(5p)     1. Desenaţi, pe foaia de examen, o piramidă patrulateră regulată dreaptă de vârf S şi 

                bază MNPT

(5p)     2. Se dau mulţimile A=\(\left\{ \text{x }\in \mathbb{R}\left| \frac{\text{1+3x}}{\text{3}} \right.\text{ 4} \right\}\) şi B=\(\left\{ x\in {{\mathbb{N}}^{*}}\left| 12\vdots x \right. \right\}\). Enumeraţi

               elementele mulţimii A\(\cap \)B.

(5p)     3. Dacă adunăm o pătrime dintr-un număr cu o optime din el şi scădem apoi o

               şaisprezecime, se obţine 17,5. Care a fost numărul iniţial.

           4. Fie f: \(\mathbb{R}\to \mathbb{R},\) f(x)=ax+b, a,b\(\in \mathbb{R}\)

(5p)    a)  Determinaţi a şi b astfel încât A(0,-3) şi B(2,1) aparţin graficului funcţiei.

(5p)    b) Pentru a=2 şi b=-3 stabiliţi dacă există puncte care au coordonate egale.

(5p)     5. Arătaţi că numărul N=\(\left( \frac{1}{\sqrt{2}+1}+\frac{1}{3+\sqrt{2}}-\frac{47}{7(6\sqrt{2}+5)} \right)\cdot 7\)este natural.

 

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

       

1. O ladă din lemn în formă de paralelipiped dreptunghic, cu lungimea de 6m, lăţimea 

   de 5m şi înălţimea de 4m se tapetează pe părţile laterale cu folie din plastic pentru a  

   se umple cu nisip.

(5p)  a) Calculaţi câţi m liniari de folie trebuie cumpărată pentru tapetare, dacă folia are o

             lăţime de 2m.

(5p)  b) Câţi m\(^{3}\)de nisip se pot pune în ladă pentru a fi plină.

(5p)  c) Dacă în ladă se pun doar 75m\(^{3}\) de nisip, calculaţi înălţimea la care se ridică nisipul în

             ladă.

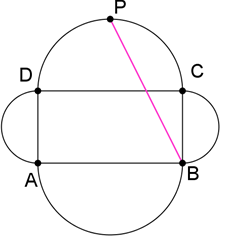
          2. Figura 3. reprezintă schiţa unui teren de joacă pentru copii, format dintr-un                 

             dreptunghi ABCD care are lungimea de 40m şi lăţimea de 20m şi din patru 

             semicercuri de diametre AB, BC, CD, DA. Punctul P este mijlocul

             semicercului de diametru DC.

(5p)  a) Ştiind că terenul este înconjurat de un gard, calculaţi lungimea gardului care-l

             înconjoară.

(5p)  b) Calculaţi suprafaţa (aria) terenului şi verificaţi dacă este mai mică decât

             2400m\(^{2}\)(3,14<\(\pi \)<3,15).

(5p)  c) Dacă în punctul B este amplasată o cişmea, iar Ciprian se află în punctul P,

            calculaţi lungimea drumului pe care-l parcurge Ciprian până cişmea.

 

 

figura 3.

 

---