Varianta 35

Prof: Bulgăr Delia Valentina

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Dacă A=1-2+3-4+5 şi B=\({{2011}^{0}}+{{1}^{2011}}\), atunci \(\frac{A}{B}\) este egal cu…………

(5p)     2. Un elev a rezolvat în 5 zile jumătate din tema de vacanţă. Lucrând în acelaşi ritm el 

                va termina tema în……….zile.

(5p)     3. Ciprian şi Andrei joacă „Nu te supăra frate!”. Probabilitatea ca la o aruncare a

               zarului să cadă faţa cu 6 puncte este……… 

(5p)     4. Un triunghi dreptunghic cu catetele de 3cm şi 4cm are lungimea înălţimii

               corespunzătoare ipotenuzei egală cu………cm.

(5p)     5. Se consideră piramida patrulateră regulată dreaptă din figura 1., în care VA=AB.

               Măsura unghiului dintre dreptele VA şi BC este egală cu ……….\(^{\circ }\).

figura 1.

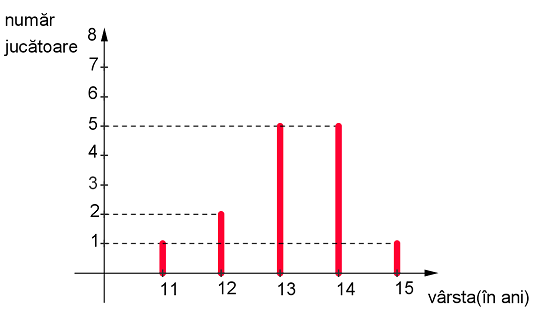
(5p)     6. În graficul de mai jos sunt reprezentate vârstele jucătoarelor din lotul de handbal al

               şcolii. Numărul jucătoarelor din lot este egal cu……………...

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

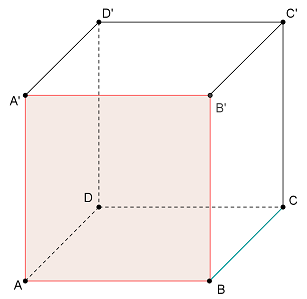
(5p)     1. Desenaţi, pe foaia de examen, prisma triunghiulară regulată dreaptă ABCA’B’C’.

(5p)     2. Arătaţi că numărul \(a=\sqrt{{{3}^{-2}}+{{2}^{-4}}}\)este din intervalul (\(\frac{1}{3},\frac{1}{2}\)).

(5p)     3. Preţul unei poşete este mai mare de 100 lei. Mădălina cumpărând un număr par de

               poşete şi două rujuri cu 25 lei bucata, achită la casierie suma de 340 lei. Cât costă o  

               poşetă?

            4. Fie funcţia f:\(\mathbb{R}\to \mathbb{R}\), f(x)=mx-3.

(5p)    a) Pentru m=2, reprezentaţi grafic funcţia f.

(5p)    b) Determinaţi m>0, ştiind că aria triunghiului format de graficul funcţiei f şi axele 

               de coordonate este 4,5.

(5p)     5. Arătaţi că suma S=\({{(3x-\sqrt{7})}^{2}}+2(\sqrt{7}+3x)(\sqrt{7}-3x)+{{(3x+\sqrt{7})}^{2}}\)nu depinde de

                numărul real x.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. O cutie de carton sub forma unei prisme patrulatere regulate este plină cu 16 cuburi de

      lemn cu latura de 3cm, aşezate pe un singur rând, fără suprapunere.

 (5p)  a) Calculaţi volumul cutiei.

 (5p)  b) De câte cuburi cu latura de 3cm are nevoie un copil pentru a construi un cub mai 

              mare cu latura de 6cm?

 (5p)  c) Pe cubul FURNICAT cu latura de 6cm, o furnică porneşte din vârful F şi ajunge în

              vârful I traversând toate feţele. Ce lungime are cel mai scurt drum posibil parcurs de 

              furnică?

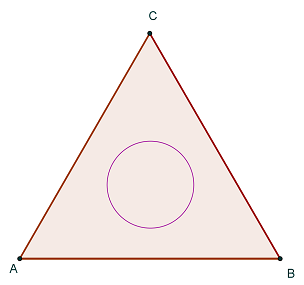
  2.  Figura 2. reprezintă suprafaţa unui teren sub formă de triunghi echilateral cu latura de 

             100m, care este ocupată în partea centrală de o grădină de legume în formă de disc

             circular cu raza de 20m, al cărui centru este în centrul de greutate al triunghiului. Pe 

             restul suprafeţei este gazon .

(5p)  a) Ce suprafaţă este cultivată cu legume (\(\pi \approx 3,15\))?

(5p)  b) Ce suprafaţă este acoperită cu gazon(\(\sqrt{3}\approx 1,74\))?

(5p)  c) Arătaţi că distanţa de la orice punct  din interiorul terenului la centrul cercului este  

            mai mică decât \(\frac{100\sqrt{3}}{3}m\).

figura 2.