Varianta 36

Prof: Burlăciuc Maria

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului 999999 : 99 este egal cu .......

(5p)     2. Rădăcina pătrată a numărului \(\sqrt{81}\) este egală cu  …..

(5p)     3. Dacă numerele a, b şi c sunt direct proporţionale cu 2; 3 şi 5, iar a∙b∙c = 240, atunci suma numerelor a şi c este  ………………………. 

(5p)     4. Aria unui trapez isoscel ortodiagonal cu lungimea liniei mijlocii de 11 cm este  .......... cm²

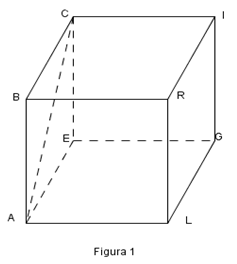
(5p)     5. În Figura 1 este reprezentat un cub ALGEBRIC.  Unghiului format de dreptele AC şi EG are măsura de .............^o

(5p)     6. În tabelul de mai jos sunt reprezentate notele obţinute de elevii clasei a VIII-a A la teza de matematică.

 Numărul elevilor care au obţinut note mai mici decât 5 este .....................

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o piramidă triunghiulară regulată STEA. 

(5p)     2. La un concurs de matematică fiecare elev a rezolvat toate cele 30 de probleme propuse. Pentru fiecare problemă rezolvată corect s-au acordat 3 puncte, pentru fiecare problemă rezolvată greşit s-au scăzut 0,75 puncte, iar din oficiu s-au acordat 10 puncte. Determinaţi punctajul obţinut de un elev care a rezolvat corect doar 12 probleme. 

(5p)    3. Calculaţi media geometrică a numerelor \(a=4\sqrt{3}+\sqrt{23}\) şi \(b=4\sqrt{3}-\sqrt{23}\).

           4. Fie expresia:

   \(E(x)=\frac{2}{{{x}^{2}}+3x}\cdot {{\left[ \left( \frac{x}{x+2}+\frac{3}{2-x}+\frac{12}{{{x}^{2}}-4} \right):\frac{{{x}^{3}}-9x}{{{x}^{2}}+4x+4} \right]}^{-1}}\)cu \(x\in {{R}^{*}}-\left\{ -3;-2;2;3 \right\}\). 

(5p)    a) Arătaţi că \(\frac{x}{x+2}+\frac{3}{2-x}+\frac{12}{{{x}^{2}}-4}\)=\(\frac{x-3}{x+2}\) . 

(5p)    b) Determinaţi mulţimea \(A=\left\{ x\in Z/E(x)\in Z \right\}\). 

(5p)     5.  Arătaţi că \(A=7\cdot {{3}^{2n+1}}\cdot {{4}^{n}}+{{9}^{n+1}}\cdot {{2}^{2n+3}}\)este divizibil cu 31.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

  1. Într-o cutie în formă de paralelipiped dreptunghic cu dimensiunile de 2 cm, 4 cm şi 6 cm, Ioana a aşezat bucăţele de zahăr cubic (în formă de cub) cu latura de 2 cm până a umplut cutia.  

 (5p)  a) Determinaţi volumul cutiei.

 (5p)  b) Câte bucăţele de zahăr cubic a aşezat Ioana în cutie?

 (5p)  c) În fiecare zi, Ioana consumă la o ceaşcă de ceai jumătate de cubuleţ de zahăr şi bea o singură ceaşcă de ceai pe zi . Ce procent din cantitatea iniţială de zahăr mai are după 4 zile?

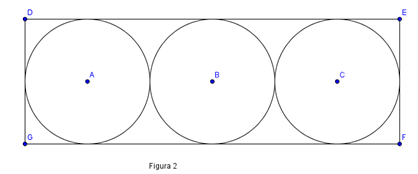
          2. Pe un carton în formă dreptunghiulară, Mihai a desenat trei cercuri de centre A, B, C şi rază 2 cm, tangente între ele şi tangente la laturile dreptunghiului DEFG, ca în Figura 2. 

(5p)  a) Determinaţi perimetrul dreptunghiului DEFG. 

(5p)  b) Determinaţi valoarea sinusului unghiului ADB. 

(5p)  c) Determinaţi suprafaţa de carton rămasă după înlăturarea celor trei cercuri, rotunjiţi la unităţi ( \(\pi \approx 3,14\)).