Varianta 37

Prof: Burlăciuc Maria

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

 (5p)    1. Dacă A = {xÎZ / xÎ(-3; 2]}, atunci card A =….

(5p)     2. Scris ca fracţie ordinară ireductibilă, numărul 0,(45) este egal cu ..............................

(5p)     3. Fie f:R\(\to \)R, f(x) = 4-2x. Punctul de intersecţie dintre graficul funcţiei f şi axa Oy are coordonatele (......;.......)

 (5p)     4. Dacă aria triunghiului ABC este de 36 cm², iar M este mijlocul laturii AC, atunci aria triunghiului ABM este egală cu .................. dm²

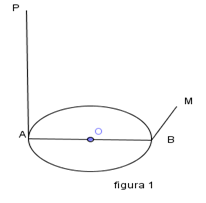
(5p)     5. Pe planul cercului de centru O şi rază OA= 3 cm se ridică perpendiculara AP= 8 cm. Dacă B este punct diametral opus punctului A, iar BM este tangentă la cerc (figura 1), atunci distanţa de la punctul P la dreapta BM este egală cu ......................... cm.

(5p)     6. Într-o urnă sunt 10 bile albe, 12 bile roşii şi 7 bile albastre. Extragem din urnă o singură bilă. Probabilitatea ca bila extrasă să fie roşie sau albastră este egală cu ...........

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un trunchi de piramidă patrulateră regulată ABCDA’B’C’D’. 

(5p)     2.Determinaţi perechile de numere naturale (a,b) ştiind că cel mai mare divizor comun al numerelor a şi b este 11, iar 2a+5b = 176. 

(5p)     3. Calculaţi 13a + 21b + 2c, ştiind că 3a+4b+c = 14 şi 2a-b+3c = 9, unde a,b,c \(\in \) R. 

           4. Fie \(x=\sqrt{37+12\sqrt{7}}+\sqrt{{{\left( 3-2\sqrt{7} \right)}^{2}}}\). 

(5p)    a) Arătaţi că \(\sqrt{37+12\sqrt{7}}\) =\(3+2\sqrt{7}\) 

(5p)    b) Calculaţi \({{\left( x-4\sqrt{7}-1 \right)}^{2012}}\). 

(5p)     5.Determinaţi funcţia f: R \(\to \)R, f(x) = (a-1)x+b+2 al cărei grafic trece prin punctele A(-1;-2) şi B(1;4).

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

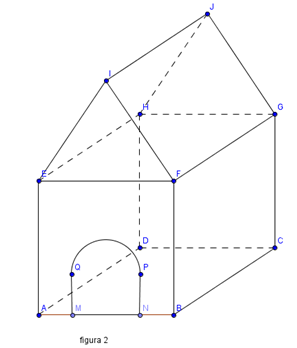
  1. Pentru a construi o cuşcă pentru Azorel, Mihai confecţionează un paralelipiped dreptunghic ABCDEFGH cu AB = AE = 0,8 m şi BC= 1 m de la care a înlăturat baza EFGH, iar pentru acoperiş foloseşte o prisma triunghiulara regulata EFIHGJ din care a înlăturat faţa laterală EFGH , iar uşa MNPQ este formată dintr-un dreptunghi cu MN = 0,6 m, NP=0,3 m şi un semicerc (figura 2).

 (5p)  a)  Determinaţi volumul cuştii. 

 (5p)  b) Determinaţi câţi cm² de material sunt necesari pentru a confecţiona uşa (\(\pi \approx 3,14\)). 

 (5p)  c) Mihai trebuie să vopsească pereţii exteriori (inclusiv uşa)  cuştii lui Azorel (nu vopseşte acoperişul). Dacă pentru 1 m² sunt necesari 0,3 litri de vopsea, determinaţi câţi litri de vopsea sunt necesari pentru vopsire.

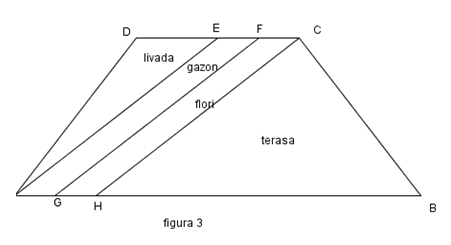
          2. Un teren  în formă de trapez isoscel ABCD cu AB=24 m şi BC =12 m a fost parcelat ca în figura 3 astfel încât HC\(\bot \)BC,  AE // GF // HC şi AG=GH= 2 m. 

(5p)  a) Determinaţi câţi metri de gard sunt necesari pentru a separa parcela de gazon de parcela de flori (gardul se montează pe segmentul GF ).

(5p)  b) Determinaţi suprafaţa ADE ocupată de livadă.

(5p)  c) Determinaţi cât costă gresia necesară pentru a placa suprafaţa terasei ştiind că 1 m² de gresie costă 40 lei, iar pierderile reprezintă 10% din cantitatea necesară.