Varianta 39

Prof: Burlăciuc Maria

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.  ( 30 de puncte)

(5p)     1. Rezultatul calculului 0,(37)∙99 este egal cu  .....…

(5p)     2. Dacă \(\left( 2x+3 \right)\in \left( -3;7 \right]\), atunci  \(x\in \left( .......;........ \right]\)

(5p)     3. Dacă 10 muncitori termină o lucrare în 8 zile, atunci 5 muncitori vor termina aceeaşi lucrare în ……… zile. 

(5p)     4. Dacă apotema unui triunghi echilateral are lungimea egală cu\(3\sqrt{3}\) cm, atunci aria triunghiului este ...............  cm² 

(5p)     5. Dacă volumul unui cub este  64 cm³, atunci lungimea diagonalei cubului este egală cu ……… cm

(5p)     6. Dacă a+b = 7 şi a∙b = 10, atunci expresia a² + b² este egală cu ..................................

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, un trunchi de piramidă triunghiulară regulată ABCA’B’C’.

(5p)     2. Mimi are un coş în care sunt cel mult 150 mere. Determinaţi câte mere are Mimi în coş ştiind că dacă le numără câte 10, câte 14 sau câte 20, rămân de fiecare dată 9 mere în coş. 

(5p)     3. Fie numerele a,b,c invers proporţionale cu 0,(3); 6^-1; 0,5. Arătaţi că a² +b² +c² este pătratul unui număr. 

           4. Fie \(f:R\to R,\text{ }f\left( x \right)=ax+b\text{ cu }a,b\in R\).

(5p)    a) Determinaţi funcţia \(f\)ştiind că \(a\)  şi  \(b\)sunt soluţiile sistemului de ecuaţii:         

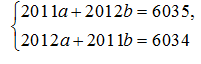
(5p)    b) Pentru\(a\)=1 şi \(b\)=2, determinaţi aria triunghiului format de graficul funcţiei \(f\)cu axele de coordonate. 

(5p)     5. Arătaţi că A = \(\sqrt{\left( n+2 \right)\left( n+3 \right)\left( n+4 \right)\left( n+5 \right)+1}\) este număr natural, \(\forall n\in \)N.

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

  1. Se consideră  o piramidă patrulateră regulată VABCD cu AB = 10 cm şi măsura unghiului format de muchia laterală  cu planul bazei  de 45^o. 

 (5p)  a) Determinaţi volumul piramidei. 

 (5p)  b) Determinaţi valoarea sinusului unghiului determinat de două feţe laterale alăturate. 

 (5p)  c) O furnică pleacă din punctul B şi merge pe suprafaţa laterală a piramidei traversând muchia VC până ajunge în punctul D, pe drumul cel mai scurt. Determinaţi lungimea drumului.

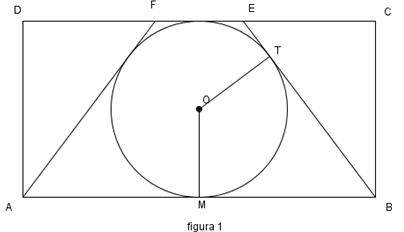
          2. Pe latura CD a dreptunghiului ABCD se consideră punctele E şi F astfel încât CE=DF. Se consideră un cerc de centru O înscris în trapezul ABEF şi se notează cu M respectiv T punctele de tangenţă cu laturile AB şi BE ca în figura 1. Se ştie că BT= 12 cm şi \(m\left( \sphericalangle TOM \right)={{120}^{o}}\).

(5p)  a) Determinaţi aria dreptunghiului ABCD.

(5p)  b) Determinaţi lungimea cercului şi aria sectorului de cerc determinat de arcul mic \(\overset\frown{TM}\) .

(5p)  c) Determinaţi aria trapezului ABEF.