Varianta 44

Prof: Ileana Cernovici

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Soluţia ecuaţiei :\(5-2\left( 1-x \right)=-x\) este…

(5p)     2.Dintre numerele \(a={{\left( 1+\sqrt{2} \right)}^{2}}\)şi \(b=2+\sqrt{2}\), este mai mare numărul...

(5p)     3. Se consideră funcţia \(f:\mathbb{R}\to \mathbb{R}\),\(f\left( x \right)=3\left( x-2 \right)+5\).Valoarea funcţiei \(f\)pentru \(x=2\) este...

 (5p)    4. Suma ariilor tuturor feţelor unui cub cu muchia de 10 cm este egală cu ...\(c{{m}^{2}}\).

(5p)     5. Cheltuielile făcute de o gospodină timp de o săptămână sunt trecute în tabelul de mai jos .Suma cheltuită în medie pe zi este de ...lei.  

              (exprimaţi suma cu două zecimale)

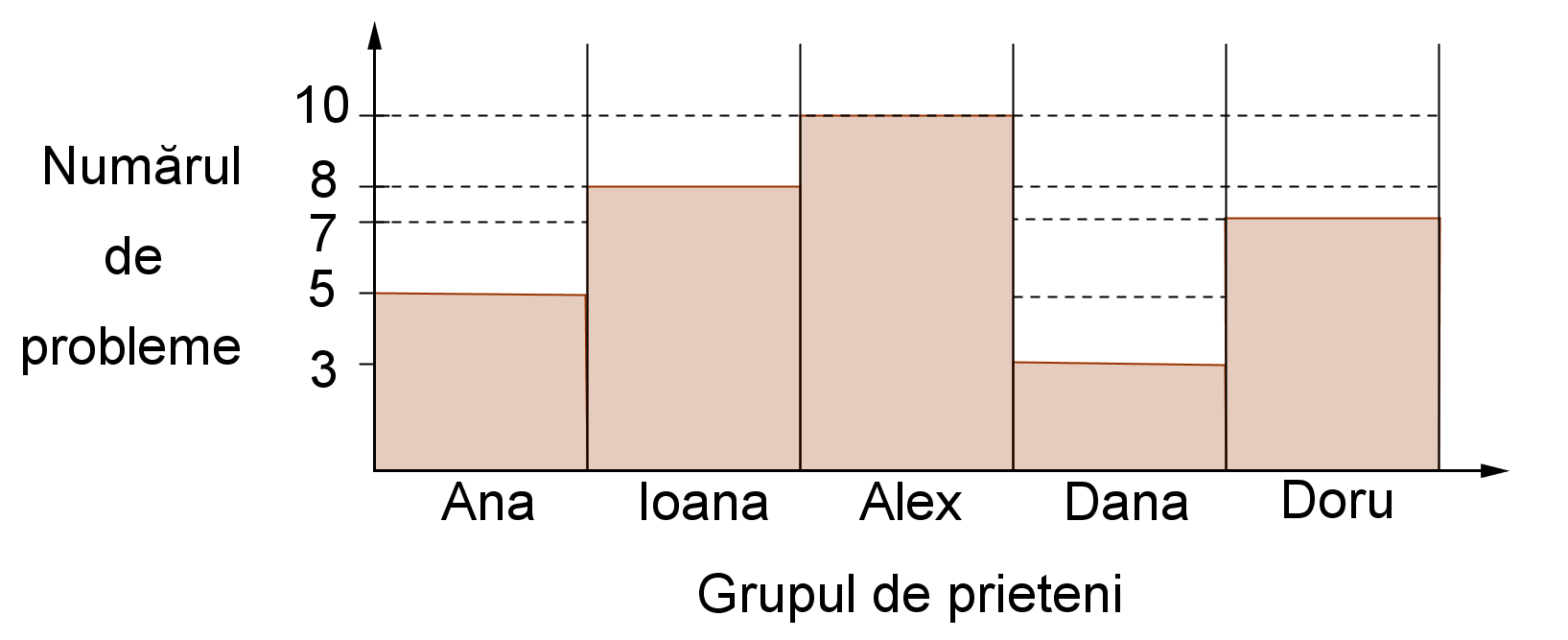
(5p)     6.Un grup de prieteni au rezolvat fiecare un număr de probleme de matematică . Numărul de probleme este trecut în graficul de mai jos. În total au rezolvat......probleme.

            SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi, pe foaia de examen, o piramidă patrulateră cu toate muchiile congruente.

(5p)     2. Aflaţi măsurile a două unghiuri complementare, ştiind că măsura unuia este cu \({{20}^{{}^\circ }}\) mai mare decât o pătrime din măsura celuilalt.

(5p)     3. Se dau numerele \(x=\sqrt{3}+2\)şi \(y=\frac{2}{3}+{{\left( \sqrt{3} \right)}^{-1}}\). Stabiliţi dacă \({{\left( x-1 \right)}^{2}}=6y\)

4. 4. Într-un bloc sunt 76 de camere în 28 de apartamente cu două şi respectiv cu trei camere.

(5p)        a) Calculaţi numărul apartamentelor cu 2 camere.

(5p)        b)  Cât la sută din numărul apartamentelor cu trei camere reprezintă numărul apartamentelor cu două camere?

(5p)     5. Aflaţi valorile reale ale numerelor \(x\) şi \(y\)pentru care expresia \(E\left( x \right)=\sqrt{{{x}^{2}}-4x+4}+\sqrt{9{{y}^{2}}+6y+10}\) are valoare minimă

           SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

       1.Se consideră expresia \(E\left( x \right)=\left( \frac{x}{x+1}-\frac{2}{1-x} \right):\frac{{{x}^{2}}+x+2}{{{x}^{4}}-{{x}^{2}}},\)unde \(x\in \mathbb{R}-\left\{ -1;0;1 \right\}\)

       (5p)  a) Calculaţi \(E\left( -2 \right)\)

       (5p)  b) Demonstraţi că \(E\left( x \right)={{x}^{2}},\forall x\in \mathbb{R}-\left\{ -1;0;1 \right\}\)

       (5p)  c) Determinaţi a,b\(\in \mathbb{R},\)pentru care\(E\left( a+b+2 \right)+E\left( a \right)-4b=0\)

2. Un diamant are forma unei piramide triunghiulare regulate cu înălţimea de 4 cm şi  muchia laterală de 5 cm . Diamantul este ambalat într-o cutie de cadou, de formă cubică cu muchia de 5 cm.

         (5p)   a) Calculaţi aria bazei diamantului.

         (5p)   b) Ce volum are diamantul?

        (5p)   c) Calculaţi cât la sută din volumul cutiei reprezintă volumul diamantului.