Varianta 46

Prof:Ileana Cernovici

- Toate subiectele sunt obligatorii. Se acordă 10 puncte din oficiu.

- Timpul efectiv de lucru: 2 ore.

 SUBIECTUL  I – Pe foaia de examen se trec doar rezultatele.         ( 30 de puncte)

(5p)     1. Dintre numerele \(a=4\sqrt{3}\)şi \(b=5\sqrt{2}\), este mai mare numărul...

(5p)     2. Cel mai mare număr natural, cu cifre distincte , mai mic decât 2010, este...

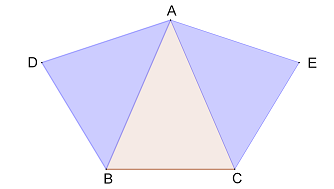
(5p)     3.  În figura de mai jos, triunghiul ABC este isoscel, \(m\left( \sphericalangle A \right)={{20}^{\circ }}\), iar triunghiurile ABD şi ACE sunt echilaterale. Măsura unghiului format de dreptele BA şi AE este...

(5p)     4. Se consideră 5 numere reale care au suma egală cu 60. Media aritmetică a lor este...

(5p)     5.  Aruncăm un zar care are feţele numerotate cu cifre de la 1 la 6. Probabilitatea ca pe faţa de sus a zarului să apară cifra 8 este egală cu...

(5p)     6. O prismă triunghiulară regulată are volumul egal cu 200 \(c{{m}^{3}}\).Dacă aria bazei este  egală cu 100\(c{{m}^{2}}\), atunci înălţimea prismei este de...

SUBIECTUL  II – Pe foaia de examen scrieţi rezolvările complete. ( 30 de puncte)

(5p)     1. Desenaţi linia mijlocie \(\left( MN \right)\), a trapezului\(ABCD\), cu\(AD\parallel BC\)

(5p)     2. Calculează valoarea expresiei \(E=a+4b+5c-719,\)dacă \(a+6b=2b+c,\)iar c=120.

(5p)     3. Un călător a parcurs un drum în trei etape: în prima etapă a parcurs 20% din întregul drum şi încă 10 km.În a doua etapă a parcurs 50% din rest şi încă 17 km, iar în a  treia etapă a parcurs ultimii 30 km.Ce lungime are întregul drum?

(5p)     4.  Se consideră prisma triunghiulară regulată \(ABC{A}'{B}'{C}'\) cu muchia bazei\(AB=6cm\) şi muchia laterală\(A{A}'=6\sqrt{3}\)cm.

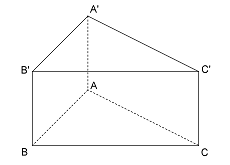
(5p)    a) Aflaţi tangenta unghiului format de dreapta \({A}'B\)cu planul\(\left( ABC \right)\)

(5p)     b) Calculaţi distanţa de la punctul C la planul \(\left( {A}'AB \right)\)

5. Arătaţi că suma \(S=7+{{7}^{2}}+{{7}^{3}}+...+{{7}^{333}}\) se divide la 57.

SUBIECTUL  III – Pe foaia de examen scrieţi rezolvările complete.( 30 de puncte)

1. Soluţia sistemului $\left\{ \begin{align}& 3x-5y=-22 \\ & 2x-y=4 \\

\end{align} \right.$, reprezintă lungimile în cm ale catetelor triunghiului \(ABC,m\left( \sphericalangle A \right)={{90}^{\circ }}\).

(5p)  a) Calculaţi aria şi perimetrul triunghiului \(ABC\)

 (5p)  b) Determinaţi lungimile proiecţiilor catetelor pe ipotenuză

 (5p)  c) Calculaţi aria cercului înscris în triunghiul \(ABC\).

2. Graficul funcţiei \(f:\mathbb{R}\to \mathbb{R},f\left( x \right)=ax+b,a\ne 0,a,b\in \mathbb{R}\)trece prin punctele \(A\left( -1;2 \right)siB\left( 2;-1 \right)\)

(5p)  a)Determinaţi funcţia \(f\left( x \right)\)şi trasaţi graficul ei.

(5p)  b) Dacă punctul \(M\left( -1;-1 \right)\in xOy,\)calculaţi tangenta unghiului \(ABM\), unde Aşi B sunt punctele de pe grafic.

(5p)  c)Calculaţi perimetrul şi aria triunghiului AMB.